📊 Piecewise Rejection Sampling
![Differential energy spectrum of ALPs from primordial black hole (PBH)${}^{[1]}$](https://axect.github.io/posts/images/006_01_test_dist.png)
Differential energy spectrum of ALPs from primordial black hole (PBH)${}^{[1]}$
누군가 위와 같이 정규화 되지 않은 확률밀도함수 그래프를 가져왔다고 가정해봅시다. 그러고서는 당신에게 이러한 확률분포를 갖는 데이터 10000개를 만들어달라고 부탁한다면, 어떻게 해야할까요?
일단, 임의의 확률밀도함수로부터 데이터를 샘플링 하는 방법에 대해 가장 잘 알려진 방법으로는 다음의 2가지가 있습니다.
Inverse Transform Sampling은 확률밀도함수의 누적분포함수를 구하고, 그 누적분포함수의 역함수를 구한 뒤, 그 역함수를 이용하여 데이터를 생성하는 방법입니다. 이 방법은 효율적이지만, 확률밀도함수가 어떤 형태를 갖느냐에 따라서 구하는 방법이 달라지기 때문에, 지금의 경우처럼 확률밀도함수의 정확한 꼴을 모를 때는 사용하기가 어렵습니다.${}^{[2]}$ 그러나, Rejection Sampling은 확률밀도함수가 어떤 형태를 갖느냐에 상관없이 적용할 수 있는데, 따라서 우리는 이 방법으로 시작해보겠습니다.
1. Rejection Sampling
Rejection sampling (혹은 Acceptance-rejection method)의 알고리즘은 매우 간단한 편입니다. 이를 설명하기 위해 저희가 sampling하고 싶은 확률분포의 확률밀도함수를 $f(x)$라 명명하겠습니다. 하지만 우리는 $f(x)$로부터 바로 sampling하는 방법을 모르므로 sampling 할 수 있는 확률밀도함수인 $g(x)$를 도입합니다. 이때, $g(x)$는 특정한 양의 상수 $M$에 대하여 정의역의 모든 $x$에 대하여 $f(x) \leq M \cdot g(x)$ 조건이 성립해야합니다. 이를 그림으로 나타내보면 다음과 같습니다.

입자물리에서 자주 볼 수 있는 그래프
보통 sampling하기 가장 쉬운 확률분포는 Uniform distribution(균등분포)이므로 여기서는 $g(x)=\text{Unif}(x|0,10)$으로 정의하였습니다. 또한 $f(x)$의 최댓값이 1이므로 $M=10$으로 정하여 $M\times g(x)$가 항상 $f(x)$보다 크거나 같음을 보장하였습니다. 이제 이 그래프를 이용하여 sampling하는 방법을 알아보겠습니다.
-
$y$를 $g(x)$로 부터 sampling합니다. 이 경우엔 $y$는 $\text{Unif}(x|0,10)$로부터 sampling된 값이 됩니다.
-
그렇게 추출된 $y$에 대하여 또 다른 균등분포인 $\text{Unif}(u|0,M\times g(y))$로부터 $u$를 sampling합니다. (이는 $g(x)$의 형태와 별개로 항상 균등분포를 사용합니다.)
-
만약 $u \leq f(y)$이면 $y$를 우리가 sampling하고자 하는 확률분포 $f(x)$로부터 sampling된 값으로 간주합니다. 그렇지 않으면 다시 1번으로 돌아가서 $y$를 sampling합니다.
이 sampling 방법이 Rejection sampling(기각 샘플링) 입니다. 3번에서 보다시피 $u$가 $f(y)$보다 크다면 기각하기 때문에 붙여진 이름입니다. 이 간단한 알고리즘 만으로 완전히 새로운 확률분포인 $f(x)$를 효과적으로 근사할 수 있습니다. 이를 위해 누적확률분포함수(CDF)를 살펴보겠습니다.
확률변수 $X$를 Rejection sampling으로 얻어진 확률변수라 하면, 다른 두 확률변수 $Y \sim g(y)$, $U \sim \text{Unif}(u|0, M\cdot g(y))$에 대하여 다음과 같은 관계를 얻을 수 있습니다. $$ P(X \leq x) = P\left(Y \leq x \,|\, U < f(Y)\right) $$ 우변의 조건부 확률은 $U$가 기각되지 않았을 때, $Y$가 $x$보다 작을 확률이며 이는 위의 알고리즘에서 3번과 같습니다. 이를 조건부 확률의 정의를 이용하여 변형하면 다음과 같습니다. $$ P(X \leq x) = \frac{P (Y \leq x,~U < f(Y))}{P(U < f(Y))} $$ 먼저 위 식의 분자를 확률밀도함수를 이용하여 전개해보겠습니다. $$ \begin{aligned} P(Y \leq x,U < f(Y)) &= \int P(Y \leq x,U < f(Y) | Y = y) \cdot g(y) \,dy \\ &= \int P(y \leq x,~U < f(y)) \cdot g(y) \,dy \\ &= \int 𝟙_{y \leq x} \cdot P(U < f(y))\cdot g(y) \, dy \\ &= \int_{-\infty}^x P(U < f(y)) \cdot g(y) \, dy \end{aligned} $$ 2번째 식에서 3번째로 넘어갈때는 $y \leq x$와 $U < f(y)$는 독립이라는 조건을 사용하였습니다. 이제 $U \sim \text{Unif}(u|0,\,M\cdot g(y))$이므로 $\displaystyle P(U < f(y)) = \frac{1}{M\cdot g(y)} \times (f(y) - 0)$을 대입하면 다음과 같습니다. $$ \begin{aligned} P(Y \leq x,~U < f(Y)) &= \int_{-\infty}^x \frac{f(y)}{M\cdot g(y)}\cdot g(y) \, dy \\ &= \frac{1}{M} \int_{-\infty}^x f(y) \, dy \end{aligned} $$ 이제 분모를 구해보겠습니다. $$ \begin{aligned} P(U < f(Y)) &= \int P(U < f(y)) \cdot g(y) \, dy \\ &= \int \frac{f(y)}{M\cdot g(y)} \cdot g(y) \, dy \\ &= \frac{1}{M} \int f(y) \, dy \\ &= \frac{1}{M} \end{aligned} $$ 마지막으로 분자와 분모를 나누면 다음과 같습니다. $$ P(X \leq x) = \int_{-\infty}^x f(y) \, dy $$ 이는 $f(x)$의 누적분포함수와 같습니다. 따라서 Rejection sampling으로 얻어진 확률변수 $X$의 확률밀도함수는 $f(x)$라는 것을 얻을 수 있습니다.
이제 수학적으로 증명을 마쳤으니, 이번에는 이것이 실제로 잘 작동하는지 코드를 작성해봅시다.
// Rust
use peroxide::fuga::*;
const M: f64 = 10.0;
const N: usize = 100_000;
fn main() {
// Create g(x)=Unif(x|0,10) & h(y)=Unif(y|0,M)
let g = Uniform(0.0, 10.0);
let h = Uniform(0.0, M);
// Rejection sampling
let mut x_vec = vec![0f64; N];
let mut i = 0usize;
while i < N {
let x = g.sample(1)[0];
let y = h.sample(1)[0];
if y <= f(x) { // Accept
x_vec[i] = x;
i += 1;
} else { // Reject
continue;
}
}
// ...
}
// Test function
fn f(x: f64) -> f64 {
1f64 / (x+1f64).sqrt() + 0.2 * (-(x-3f64).powi(2) / 0.2).exp()
}
알고리즘 자체가 간단하므로 코드 역시 굉장히 간단합니다. 하지만 그럼에도 결과는 뛰어납니다.
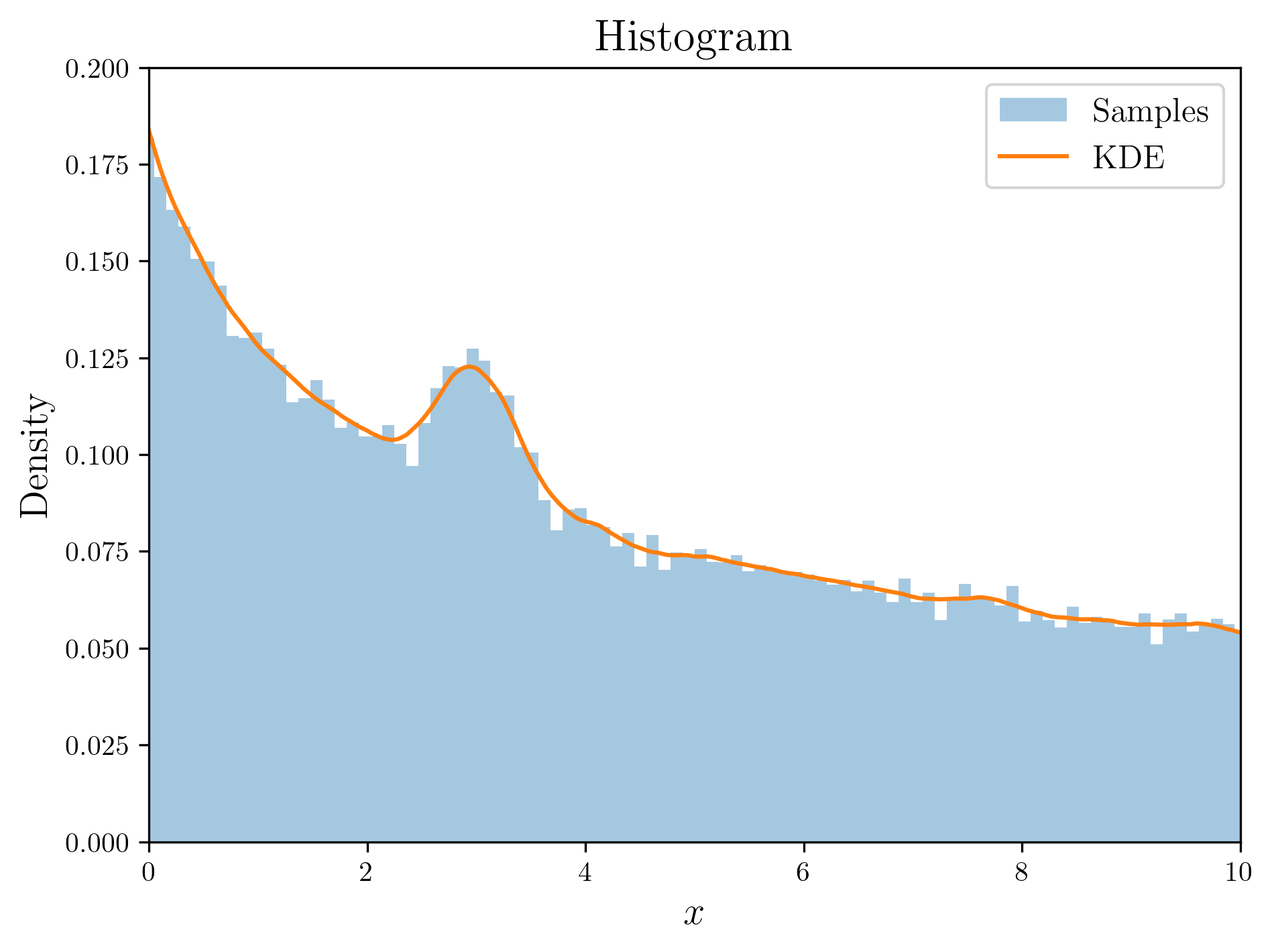
Result of rejection sampling
확률밀도함수의 형태에 구애받지 않으며 구현까지 쉬운 Rejection sampling이지만 치명적인 단점 역시 존재합니다. 바로 계산 효율이 굉장히 떨어진다는 것입니다. Rejection sampling에서 sample을 확보하려면 기각 조건에서 살아남아야 합니다. 이는 즉, $P(U < f(Y))$가 높을 수록 빠르게 sample을 확보할 수 있다는 것이고 반대로 낮을 수록 충분한 수의 sample을 확보하기까지 오래 걸린다는 것입니다. 이를 Acceptance rate (승인 비율)라고 하며 이는 이미 위의 증명에서 계산하였습니다.
Acceptance rate
저희가 사용한 알고리즘에서는 이는 $1/M$과 같고, 이는 $f(x)$가 차지하는 넓이를 $M \cdot g(x)$가 차지하는 전체 넓이로 나눈 것과 같습니다. 따라서 분포간의 차이가 크면 클수록 Acceptance rate가 낮아지고 그만큼 sample을 확보하는데 오랜 시간이 걸린다는 것입니다. 그나마 저희가 사용한 예시는 $g(x)$와 $f(x)$의 차이가 큰 부분이 많지 않아서 비교적 괜찮습니다만, 시작할 때 제시하였던 확률분포처럼 0인 부분이 많은 경우에는 $g(x)$로 Uniform distribution을 사용한다면 대부분 기각되어버리기 때문에 시간이 오래걸릴뿐더러 거의 0 근처의 tail에 대해서는 sampling이 불가능한 지경에까지 이를 수 있습니다. 그렇다면 어떻게 이를 해결할 수 있을까요?
2. Piecewise Rejection Sampling
사실 이미 연구자들은 이런 경우를 위해 여러가지 방법을 고안해두었습니다. 대표적으로 Adaptive Rejection Sampling (ARS) 와 Adaptive Rejection Metropolis Sampling (ARMS) 가 있습니다. 전자의 경우는 효율적이지만 함수가 반드시 로그-오목(log-concave)하다는 보장이 있어야 하고 후자의 경우는 이를 해결하여 일반화했지만 구현이 상당히 어렵습니다. 물론 이미 잘 만들어진 R package 등이 있으니 사용하는 것 자체는 어렵지 않습니다만, 여기서는 더 간단한 방법을 소개하고자 합니다. 바로 Piecewise Rejection Sampling (PRS) 입니다. 이는 제가 물리학 연구를 수행하던 중에 처음에 제시한 문제를 해결하고자 만든 방법으로, 기본적인 토대는 Rejection sampling과 같지만 $g(x)$를 단순한 Uniform distribution이 아닌 $f(x)$에 최적화된 Weighted uniform distribution (가중균등분포)로 상정하는 방법입니다. 이를 차근차근 설명해보겠습니다.
2.1. Max-Pooling
아마 딥러닝에 관심있는 사람이라면 Max Pooling 이라는 개념을 익히 들어봤을겁니다. CNN에서 자주 사용되는 Max pooling은 사실 개념은 굉장히 간단합니다. 일단 Max pooling의 수학적 정의는 다음과 같습니다.
Max pooling
Let $f\,:\,[a,b]\to \mathbb{R}$ be a continuous function and consider the equidistant partition of the interval $[a,b]$ $$ a = x_0 < x_1 < \cdots < x_{n-1} < x_n = b $$ The partitions size, $(b-a)/n$ is called stride. Denote by $\displaystyle M_i = \max_{[x_{i-1},x_i]}f(x)$ and consider the simple function
$$ S_n(x) = \sum_{i=1}^n M_i 𝟙_{[x_{i-1},x_i)}(x). $$
The process of approximating the function $f(x)$ by the simple function $S_n(x)$ is called max-pooling.
여기서 사용한 simple function이란 측도론(Measure theory)에서 등장하는 함수로 각 구간에서 서로 다른 상수를 가지는 함수를 말합니다. 자세한 정의는 Precise Machine Learning with Rust의 Definition 10과 Property 1을 참고하시면 됩니다.
결국 Max-pooling이란 간단히 말해 $f(x)$를 $n$개의 구간으로 나누고 각 구간에서 $f(x)$의 최대값을 구하여 이를 각 구간에서의 대푯값(Representative value)으로 갖는 simple function을 구하는 것입니다. 이를 처음 제시한 분포에 대해 적용해보면 다음과 같습니다.

Max-pooling for Test Distribution
그림의 빨간색 실선을 $f(x)$라 하면 파란색 점선은 $f(x)$를 max-pooling한 결과입니다. 이쯤되면 이미 눈치챈 분들도 있을텐데, 저희는 이 파란색 점선을 Rejection sampling에서의 $M\cdot g(x)$로 사용할 것입니다. 이를 위해 우리는 각 구간별로는 균등분포의 형태를 갖지만 각각 다른 대푯값을 갖는 확률분포를 정의할 것입니다. 이것이 바로 위에서 언급했던 Weighted uniform distribution (가중균등분포)입니다.
2.2. Weighted Uniform Distribution
Weighted uniform distribution
정의는 뭔가 복잡해 보이지만, 이를 1차원 구간에 대해서 정의하면 굉장히 간단하다는 것을 알 수 있습니다.
- $S = [a,b]$
- $\mathcal{A} = \left\{[x_{i-1},x_i)\right\}_{i=1}^n$ and $\Delta x_i \equiv x_i - x_{i-1}$
- $\displaystyle \text{WUnif}(x|\mathbf{M}, \mathcal{A}) = \frac{1}{\sum_{j}M_j \cdot \Delta x_j}\sum_i M_i 𝟙_{A_i}(x)$
여기서는 어차피 저희가 사용할 분포가 1차원 분포이므로 앞으로 이 정의를 이용하여 계산을 진행하겠습니다. 일단, 이 함수가 확률밀도함수임은 간단히 증명할 수 있습니다.
$$ \begin{aligned} \int_a^b \text{WUnif}(x|\mathbf{M}, \mathcal{A}) dx &= \int_a^b \frac{1}{\sum_{j}M_j \cdot \Delta x_j}\sum_i M_i 𝟙_{A_i}(x) dx \\ &= \frac{1}{\sum_{j}M_j \cdot \Delta x_j}\sum_i M_i \int_{a}^{b} 𝟙_{A_i}(x) dx \\ &= \frac{1}{\sum_{j}M_j \cdot \Delta x_j}\sum_i M_i \cdot \Delta x_i \\ &= 1 \end{aligned} $$
Weighted uniform distribution은 sampling하기도 쉽습니다. sampling 방법은 다음과 같습니다.
-
전체 $n$개의 구간 중에서 한 구간을 뽑습니다. 이때 각 구간의 확률은 $\displaystyle \frac{M_i \cdot \Delta x_i}{\sum_{j}M_j \cdot \Delta x_j}$입니다.
-
각 구간은 Uniform distribution을 따르므로, 구간 내에서 Uniform distribution으로 하나의 샘플을 뽑습니다.
만일 max-pooling을 적용하여 $\mathbf{M}, \mathcal{A}$를 골랐다면, 각 구간의 길이가 모두 동일하므로 확률에서 구간의 길이 항이 사라집니다. 따라서 이 경우에 각 구간의 확률은 $M_i / \sum_{j}M_j$가 되어 굉장히 간단해집니다.
2.3. Piecewise Rejection Sampling
Weighted uniform distribution도 sampling방법을 알고 있는 엄연한 하나의 확률분포이므로, 이를 Rejection sampling에서의 $g(x)$로 사용할 수 있습니다. 다만, 항상 $f(x)$보다 커야된다는 조건을 만족시키기 위하여 임의의 $\mathbf{M}, \mathcal{A}$를 고르는 것이 아닌 max-pooling을 적용하여 $\mathbf{M}, \mathcal{A}$를 얻을 것입니다. 이 과정을 정리하면 다음과 같습니다.
-
전체 구간을 몇 개의 구간으로 나눌지 결정합니다. 이때, 구간의 개수를 $n$이라고 하고 각 구간의 길이를 동등하게 나누어 $\mathcal{A}$를 정의합니다.
-
나눠진 구간에 대해 $f(x)$를 max-pooling하여 $\mathbf{M}$을 얻습니다.
-
$\mathbf{M}, \mathcal{A}$를 이용하여 Weighted uniform distribution을 정의합니다.
-
이렇게 정의된 Weighted uniform distribution을 Rejection sampling에서의 $g(x)$로 사용하여 sampling합니다.
이러한 sampling 방법은 마치 구간을 나누어 sampling하는 것과 같으므로 Piecewise Rejection Sampling 으로 명명하겠습니다. 이 방법에서의 Acceptance rate를 구해보면 단순히 Uniform distribution을 사용하여 Rejection sampling을 할 때에 비해 Acceptance rate가 높아지는 것을 알 수 있습니다.
$$ \begin{aligned} P(U < f(Y)) &= \int_a^b P(U < f(Y) | Y = y) \cdot g(y) \, dy \\ &= \int_a^b P(U < f(y)) \cdot \text{WUnif}(y|\mathbf{M}, \mathcal{A}) \, dy \\ &= \frac{1}{\sum_{j}M_j \cdot \Delta x_j} \sum_i M_i \int_{A_i} P(U < f(y)) dy \end{aligned} $$ $U \sim \text{Unif}(u|0, M_i)$이고, $P(U < f(y)) = f(y)/{M_i}$이므로 다음과 같이 정리할 수 있습니다. $$ \begin{aligned} P(U < f(Y)) &= \frac{1}{\sum_{j}M_j \cdot \Delta x_j} \sum_i \int_{A_i} f(y)\, dy \\ &= \frac{1}{\sum_{j}M_j \cdot \Delta x_j} \geq \frac{1}{M_\max \cdot \sum_{j} \Delta x_j} = \frac{1}{M} \end{aligned} $$
마지막 부등식은 $M_i$ 중에서 가장 큰 값에 전체 구간의 길이를 곱하면 원래 Uniform distribution을 사용할 때의 $M$과 같다는 것을 이용하여 정리한 것입니다. 이를 통해 Piecewise rejection sampling의 Acceptance rate는 Uniform distribution을 사용할 때의 Acceptance rate보다 항상 높다는 것을 알 수 있습니다.
이제 마지막으로 처음에 제시했던 문제를 Piecewise rejection sampling을 이용하여 풀어보겠습니다. 위 알고리즘은 Rust numeric library인 Peroxide에 이미 구현이 되어 있으므로 이를 이용하겠습니다.
// Before running this code, you need to add peroxide in Cargo.toml
// `cargo add peroxide --features parquet`
use peroxide::fuga::*;
#[allow(non_snake_case)]
fn main() {
// Read parquet data file
let df = DataFrame::read_parquet("data/test.parquet").unwrap();
let E: Vec<f64> = df["E"].to_vec();
let dNdE: Vec<f64> = df["dNdE"].to_vec();
// Cubic hermite spline -> Make continuous f(x)
let cs = cubic_hermite_spline(&E, &dNdE, Quadratic);
let f = |x: f64| cs.eval(x);
// Piecewise rejection sampling
// * # samples = 10000
// * # bins = 100
// * tolerance = 1e-6
let E_sample = prs(f, 10000, (E[0], E[E.len()-1]), 100, 1e-6);
// Write parquet data file
let mut df = DataFrame::new(vec![]);
df.push("E", Series::new(E_sample));
df.write_parquet(
"data/prs.parquet",
CompressionOptions::Uncompressed
).unwrap();
}
이렇게 만들어진 데이터를 히스토그램으로 그려보면 다음과 같습니다.
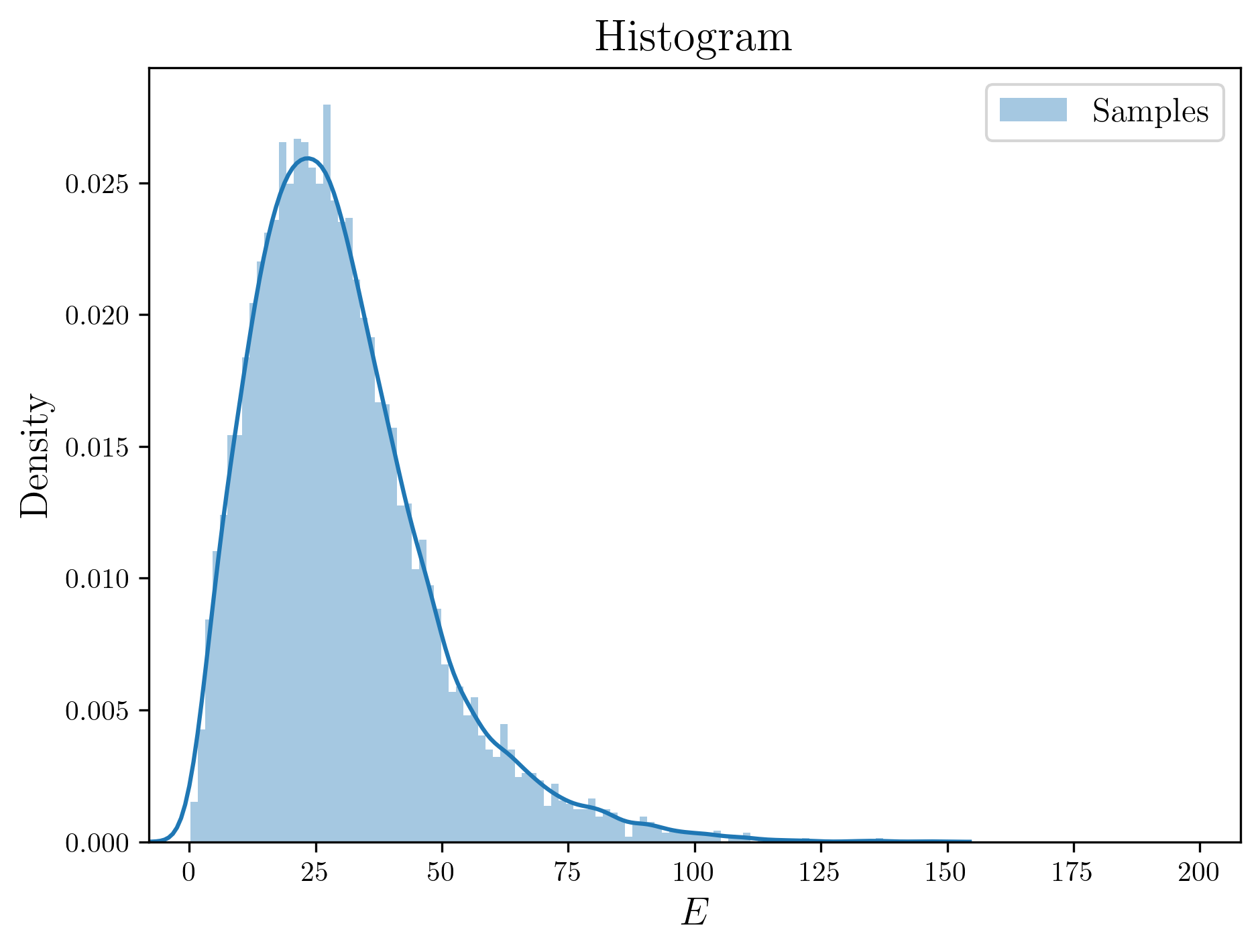
Finally, we get samples!
References
-
Yen-Chi Chen, Lecture 4: Importance Sampling and Rejection Sampling, STAT/Q SCI 403: Introduction to Resampling Methods (2017)
-
Ovidiu Calin, Deep Learning Architectures: A Mathematical Approach, Springer (2020)
-
Tae-Geun Kim (Axect), Precise Machine Learning with Rust (2019)
A. Footnotes
[1]: 여기에 사용된 그림은 원시블랙홀(Primordial Black hole; PBH)로부터 특정시간에 방출된 액시온유사입자들(Axion Like Particles; ALPs)의 스펙트럼을 그린 그림입니다. 이 연구에 대한 자세한 내용은 arXiv:2212.11977을 참고하시면 됩니다.
[2]: 물론 이 경우에도, 노드들을 cubic spline 등의 방법으로 근사하고 수치적분이나 polynomial 적분을 이용하여 누적분포함수를 구한 후, 이를 다시 interpolation이나 spline등의 방법으로 fitting한 후 역함수를 구하는 방법을 사용할 수 있긴합니다. 하지만 이는 오차가 꽤 심하고 비효율적이라 추천하진 않습니다.