💔 Decorrelation + Deep learning = Generalization

딥러닝에서 가장 빈번하게 일어나는 문제로 Overfitting (과적합) 이 있습니다. 이는 데이터가 많지 않을 때, 학습을 많이 할 수록 잘 발생하는 문제이며 이로 인하여 훈련 데이터셋에 대해서는 성능이 좋더라도 검증 데이터셋이나 실제 데이터셋에 대해서는 성능이 안 나오는 문제가 발생합니다. 이를 해결하기 위하여 사람들은 여러 방법을 고안했는데, 통계학에서는 일찌감치 Ridge나 LASSO와 같은 regularization 방법을 사용하였으며 딥러닝에서도 마찬가지로 weight을 regularize하거나 신경망에 여러 기술을 적용하는 것들을 도입하였습니다. 이러한 기술로는 다음과 같은 방법들이 있습니다.
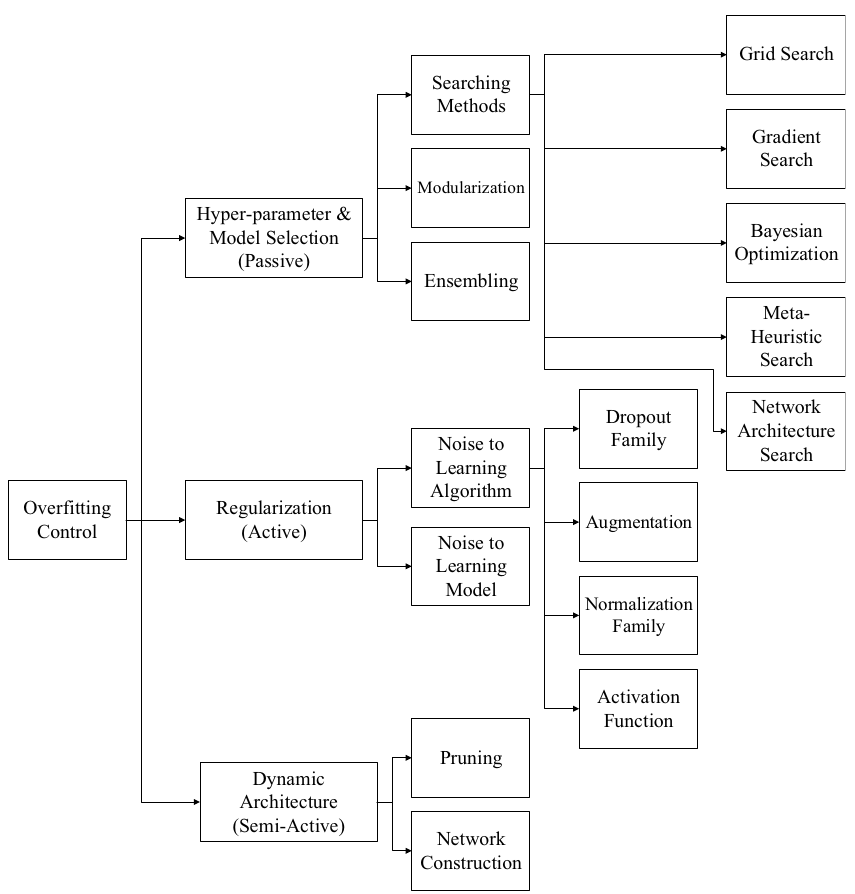
Bejani, M.M., Ghatee, M. A systematic review on overfitting control in shallow and deep neural networks. Artif Intell Rev 54, 6391–6438 (2021)
특히 이 중에서 가장 유명하다고 할 수 있는 것은 Dropout 인데, 이는 신경망의 뉴런들 중 일부를 제거함으로써 뉴런들의 중복활동을 억제하는 효과를 주는 것입니다. 실제로 이는 Overfitting을 줄일 수 있는 굉장히 효과적인 방법이었고, 이제는 신경망 구성에 포함되는 것이 당연한 정도가 되었습니다. 다만 Dropout이 모든 경우에 효과적인 방법은 아닙니다. 훈련 데이터가 적거나 뉴런 수 자체가 적다면 임의의 뉴런을 제거하는 것이 신경망의 표현력을 제한할 수 있습니다. 또한 그 효과와는 별개로 Dropout은 특유의 간단한 구조와 개념 덕에 이론적인 즐거움은 반감되는 면이 있습니다. 여기서는 그 즐거움과 효과를 보완해주는 재미있는 논문을 소개하고자 합니다.
1. Why do we need decorrelation?
1.1. Covariance & Correlation
제가 리뷰할 논문은 표지에서 보셨다시피 2015년에 발표된 Reducing Overfitting in Deep networks by Decorrelating Representations 논문입니다. 이 논문은 Decorrelation 이라는 방법으로 Overfitting을 줄이는 것에 대해 다루었는데, 이것으로 Dropout의 성능을 한층 더 끌어올릴 수 있다는 결과를 도출하였습니다. 다만 Decorrelation이라는 것이 생소하기도 하고 큰 관심을 끌지 못하는 주제라 폭발적인 반응은 끌어내지 못하였습니다만, 그래도 꾸준히 인용되고 있는 좋은 논문입니다.
Decorrelation을 이해하기 위해서는 먼저 Correlation에 대해 이해해야 합니다. Correlation은 두 데이터 간의 상관관계를 나타낸 것으로 이를 나타내는 방법에는 여러가지가 존재하는데, 가장 대표적인 방법으로는 Covariance(공분산)가 있습니다. 공분산의 정의는 2개의 확률변수의 선형 관계를 나타내는 것으로 다음과 같습니다.
$$ \text{Cov}(X,\,Y) \equiv \mathbb{E}\left[(X-\mathbb{E}[X])(Y-\mathbb{E}[Y])\right] $$
보통 공분산 값이 양수이면 두 변수는 비례 관계가 있으며 음수이면 반비례 관계가 있고, 0에 가까우면 관계가 없다고 여겨집니다. 이를 좀 더 정량화 한것으로는 Pearson correlation coefficient(피어슨 상관계수)가 있는데 이것의 정의는 다음과 같습니다.
$$ \text{Corr}(X,\,Y) \equiv \frac{\text{Cov}(X,\,Y)}{\sqrt{\text{Var}(X) \text{Var}(Y)}} $$
이렇게 정의하면 상관계수가 가질 수 있는 값의 범위가 -1에서 1까지로 한정되는데, 1에 가까울 수록 정비례 관계가 있고, -1에 가까울 수록 반비례 관계가 있으며 0에 가깝다면 상관관계가 존재하지 않는다는 것을 의미합니다. 예를 들어 다음과 같은 데이터 2개를 생각해봅시다.
# Python
import numpy as np
x = np.array([1,2,3,4])
y = np.array([5,6,7,8])
이 2개의 변수에 대한 공분산은 다음과 같은 함수로 계산할 수 있습니다.
# Python
def cov(x, y):
N = len(x)
m_x = x.mean()
m_y = y.mean()
return np.dot((x - m_x), (y - m_y)) / (N-1)
이를 이용하여 위의 x, y에 대한 공분산을 계산하면 1.6666666666666667이라는 값을 얻을 수 있는데, 양의 상관관계라는 것을 얻을 수는 있지만 값을 해석하는데는 어려움이 있습니다. 이를 깔끔히 해석하기 위하여 위에서 언급하였던 피어슨 상관계수를 정의하면 다음과 같습니다.
# Python
def pearson_corr(x, y):
# ddof=1 for sample variance
return cov(x, y) / np.sqrt(x.var(ddof=1) * y.var(ddof=1))
이를 위 데이터에 적용하면 정확히 1의 값을 가지는 것을 볼 수 있습니다. 이는 두 변수가 완벽하게 선형적으로 정비례관계에 있기 때문입니다.
여러 개의 feature들이 있다면 행렬을 만들어 이들의 공분산을 한 번에 나타낼 수 있을 것입니다. 이를 공분산행렬(Covariance matrix)이라고 부르며 다음과 같이 나타냅니다.
$$ C_{ij} = \text{Cov}(x_i,\,x_j) $$
따라서 공분산행렬은 feature의 개수와 같은 행과 열을 갖는 정사각행렬로 표현됩니다.
1.2. Overfitting & Decorrelation
딥러닝에서 갑자기 상관관계를 설명하는 까닭은 두 변수 혹은 여러 변수가 서로 유의미한 상관관계를 갖고 있다면 이것이 모델에 악영향을 끼치기 때문입니다. 심층신경망은 각 feature들에 할당된 가중치를 업데이트하며 학습하게 되는데, 만일 두 feature가 정확히 같은 역할을 한다면 둘 중 어떤 가중치를 변경해도 같은 결과가 발생하는 일종의 degeneracy가 발생하게 됩니다. 이는 정확한 학습을 방해하고 신경망을 편향시키는데, 위 논문에서는 이것이 과적합을 발생시키는 원인으로 간주하였습니다. 실제로 논문에서는 과적합 정도를 훈련 정확도와 검증 정확도의 차이로 정의하고 Decorrelation 정도를 수치화한 것을 DeCov라는 변수로 둔다면 다음과 같은 결과를 얻을 수 있음을 보였습니다.
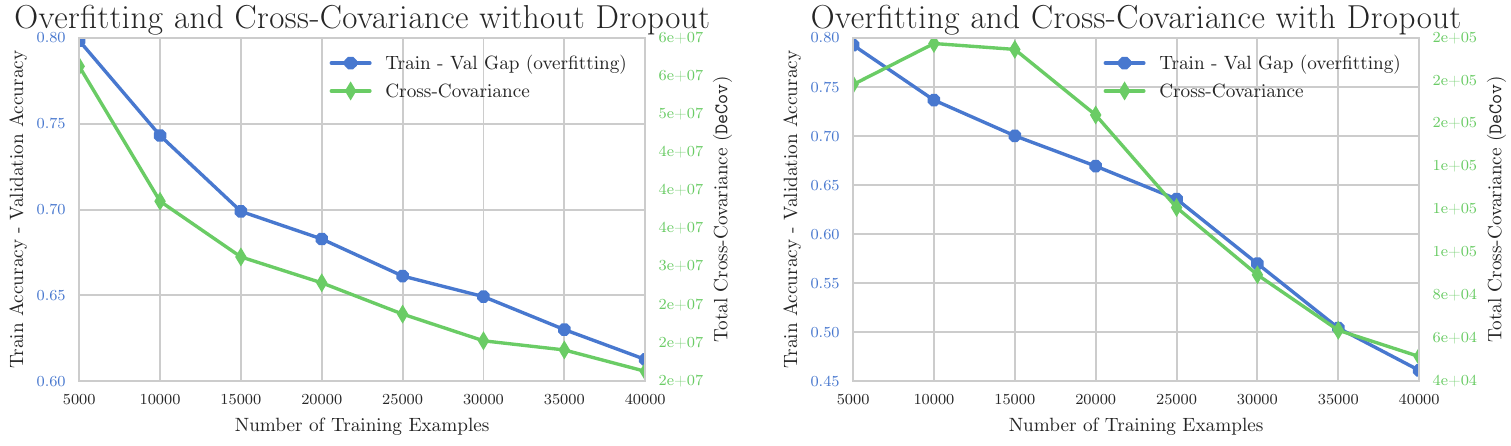
Overfitting과 Covariance의 상관관계
위 그림에서는 훈련 샘플을 늘리면서 Overfitting 정도가 작아질 때, Cross-Covariance 정도도 같이 줄어드는 것을 볼 수 있습니다. 이를 이용하면 Covariance를 줄인다면, 즉, Decorrelation을 한다면 Overfitting을 줄일 수 있을 것이라 생각할 수 있습니다.
2. How to decorrelate?
논문에서는 hidden layer의 output들을 activation한 값들을 decorrelate해야 한다고 생각하였습니다. 실제로 다음 weight들과 곱해지는 것은 이들이므로 합리적인 생각이라 할 수 있습니다. 따라서 한 hidden layer의 activation 값들을 $h^n \in \mathbb{R}^d$라고 정의하면 다음과 같이 이들의 공분산행렬을 정의할 수 있습니다. ($n$은 batch index를 의미합니다.)
$$ C_{ij} = \frac{1}{N} \sum_n (h_i^n - \mu_i)(h_j^n - \mu_j) $$
이제 이 값을 이용하여 서로의 공분산을 줄이기만 한다면 목적을 달성할 수 있습니다. 하지만, 이는 엄연히 행렬이므로 Loss 함수에 포함하려면 단순한 스칼라로 이를 표현해야할 필요가 있습니다. 논문에서는 이를 다음과 같은 Loss 함수로 표현하였습니다.
$$ \mathcal{L}_{\text{DeCov}} = \frac{1}{2}(\lVert C \rVert_F^2 - \lVert\text{diag}(C) \rVert_2^2) $$
$\lVert \cdot \rVert_F$는 행렬의 Frobenius norm을 나타낸 것이며 $\lVert \cdot \rVert_2$는 $l^2$ norm을 나타낸 것입니다. 대각성분만 따로 분리하여 뺀 까닭은 공분산행렬의 대각성분은 단순히 각 feature의 분산을 나타내는 것이라, decorrelation과 관계가 없기 때문입니다. 그렇다면 이제 이 Loss 함수를 마치 regularization 항을 추가하듯이 저희의 Loss 함수에 추가하기만 하면 Decorrelation을 구현할 수 있습니다.
그렇다면 이를 실제 딥러닝에서는 어떻게 구현할 수 있을까요? 언뜻 생각해보면 공분산행렬과 그에 따른 norm의 gradient 계산을 전부 구현하는 것은 굉장히 복잡해보이지만, 다행히 PyTorch에는 covariance matrix와 norm에 대한 자동미분이 전부 구현되어 있습니다. 따라서 다음과 같은 간단한 코드로 이를 구현할 수 있습니다.
# Python
import torch
def decov(h):
C = torch.cov(h)
C_diag = torch.diag(C, 0)
return 0.5 * (torch.norm(C, 'fro')**2 - torch.norm(C_diag, 2)**2)
3. Apply to Regression
원 논문에서는 이를 여러가지 image 데이터들에 적용해보았지만, 여기서는 그 효과를 좀 더 쉽게 실감하기 위하여 간단한 회귀문제에 적용해보고자 합니다. 신경망에게 출제할 데이터는 다음과 같습니다.
![비선형 데이터 [참고: Peroxide_Gallery]](https://axect.github.io/posts/images/005_04_data.png)
비선형 데이터 [참고: Peroxide_Gallery]
이를 간단한 신경망과 DeCov를 구현한 신경망 각각에 대해 풀어보게 하였는데, DeCov 신경망의 구조는 다음과 같습니다.
import pytorch_lightning as pl
from torch import nn
import torch.nn.functional as F
# ...
class DeCovMLP(pl.LightningModule):
def __init__(self, hparams=None):
# ...
self.fc_init = nn.Sequential(
nn.Linear(1, self.hidden_nodes),
nn.ReLU(inplace=True)
)
self.fc_mid = nn.Sequential(
nn.Linear(self.hidden_nodes, self.hidden_nodes),
nn.ReLU(inplace=True),
nn.Linear(self.hidden_nodes, self.hidden_nodes),
nn.ReLU(inplace=True),
nn.Linear(self.hidden_nodes, self.hidden_nodes),
nn.ReLU(inplace=True),
)
self.fc_final = nn.Linear(self.hidden_nodes, 1)
# ...
def forward(self, x):
x = self.fc_init(x)
x = self.fc_mid(x)
return self.fc_final(x)
def training_step(self, batch, batch_idx):
x, y = batch
h0 = self.fc_init(x)
loss_0 = decov(h0)
h1 = self.fc_mid(h0)
loss_1 = decov(h1)
y_hat = self.fc_final(h1)
loss = F.mse_loss(y,y_hat) + loss_0 + loss_1
return loss
# ...
이를 간단히 살펴보면 fc_init 단일층을 지났을 때의 값을 이용하여 loss_0를 정의하였고, fc_mid라는 3개 층을 지났을 때의 값을 이용하여 loss_1을 정의하여 이를 MSE loss에 regularization 항처럼 적용한 것을 볼 수 있습니다. 결과를 보기 전에 SimpleMLP와 DeCovMLP의 훈련과정을 보면 재미있는 것을 관측할 수 있습니다.
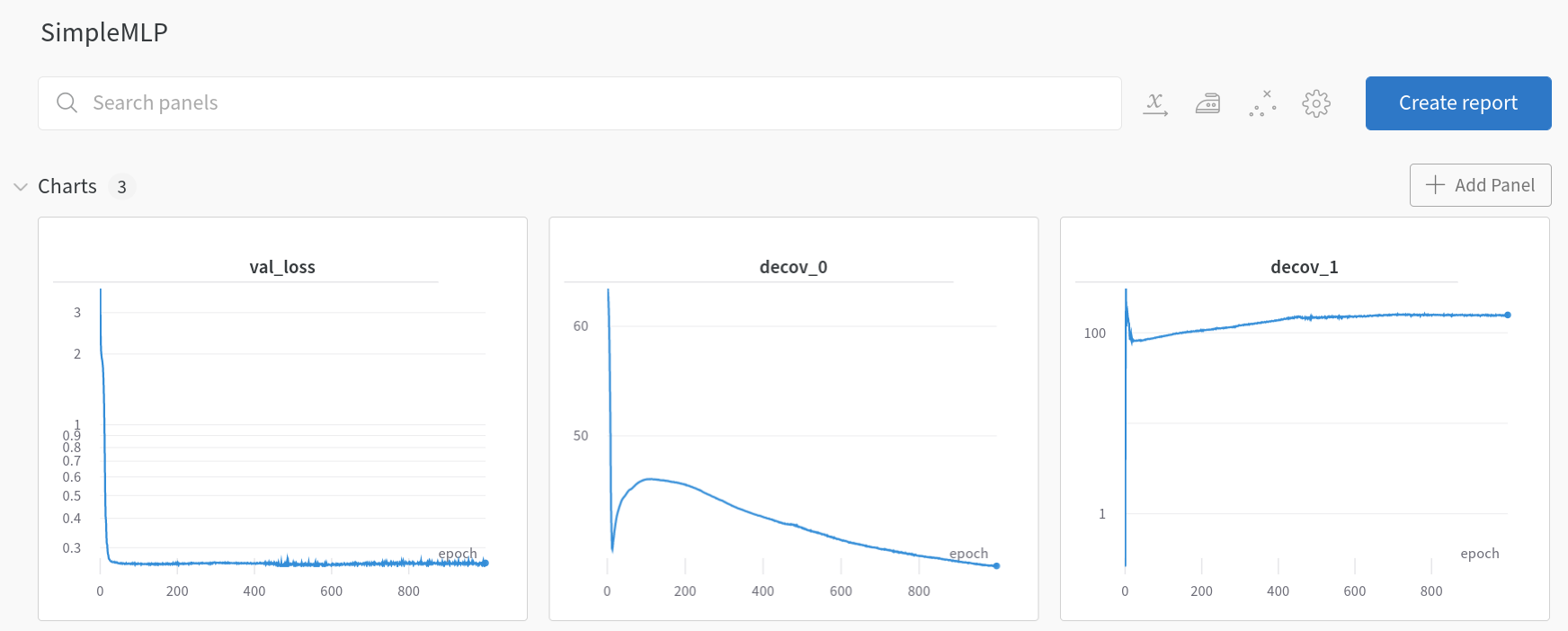
SimpleMLP losses (wandb.ai)
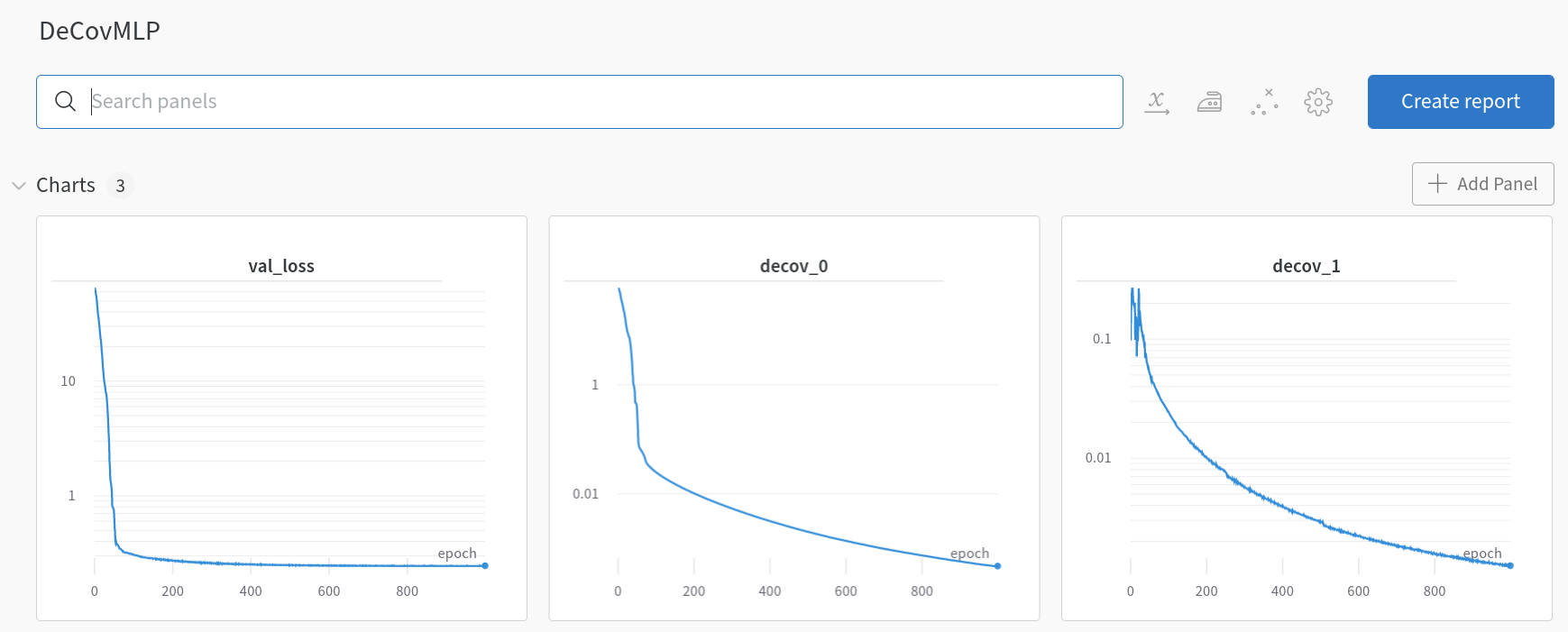
DeCovMLP losses (wandb.ai)
SimpleMLP에서는 훈련이 거듭될수록 decov_1이 증가하다 더 이상 줄어들지 않는 것을 볼 수 있습니다. 하지만 DeCovMLP에서는 decov_1의 값이 꾸준히 줄어드는 것을 볼 수 있습니다. 이는 논문에서 예상했던 것과 같이 overfitting 되면 feature 간의 correlation 역시 늘어나는 것과 같은 양상입니다. 그렇다면 이제 결과를 보도록 하겠습니다.
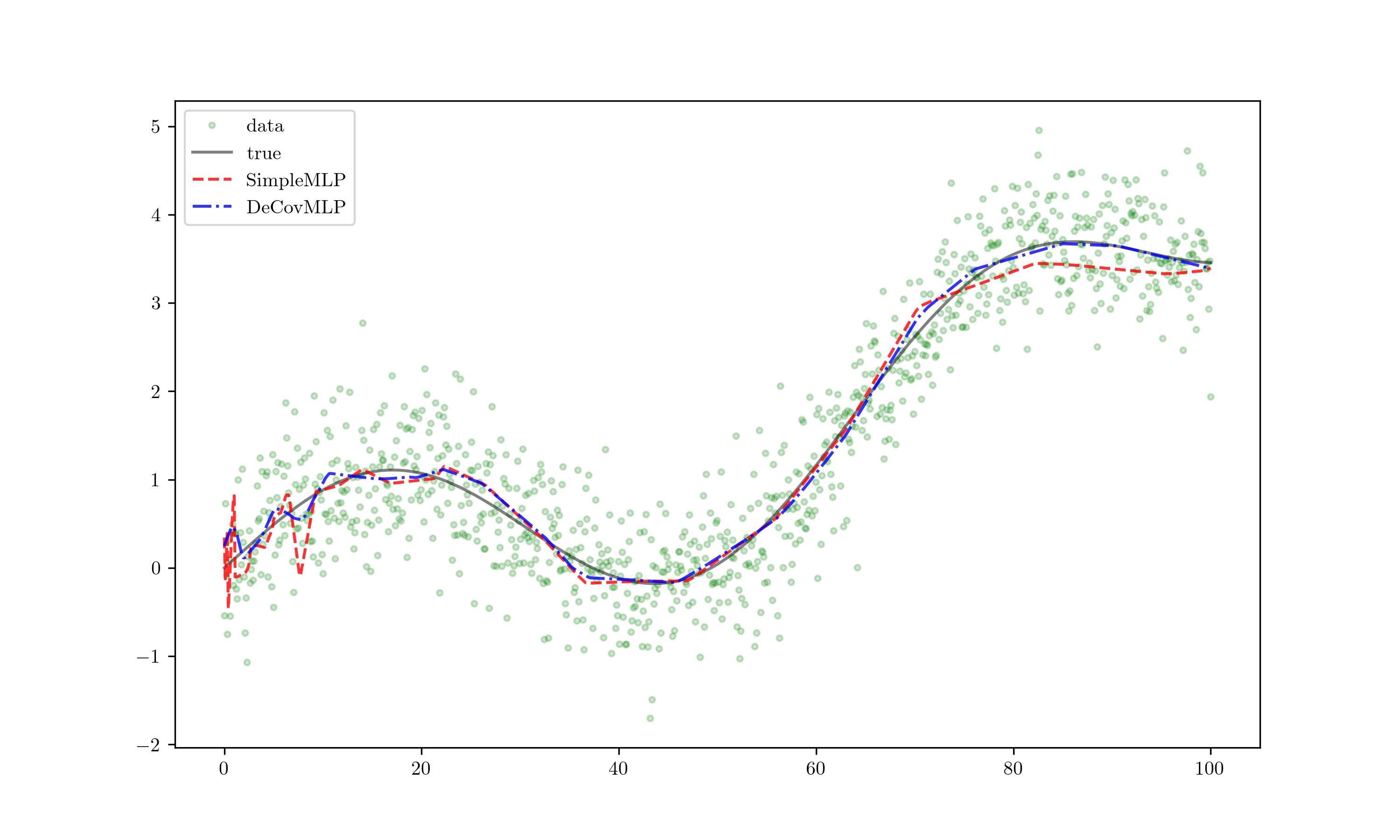
Results!
붉은 선은 SimpleMLP의 결과이고 파란 선은 DeCovMLP의 결과입니다. 붉은 선이 Overfit 되어 요동이 심한 것에 비해 파란 선은 true에서 별로 벗어나지 않고 요동도 심하지 않다는 것을 볼 수 있습니다. 여기까지만 해도 충분히 놀라운 결과이지만 조금만 extrapolate을 해보면 더 재미있는 결과를 얻을 수 있었습니다.
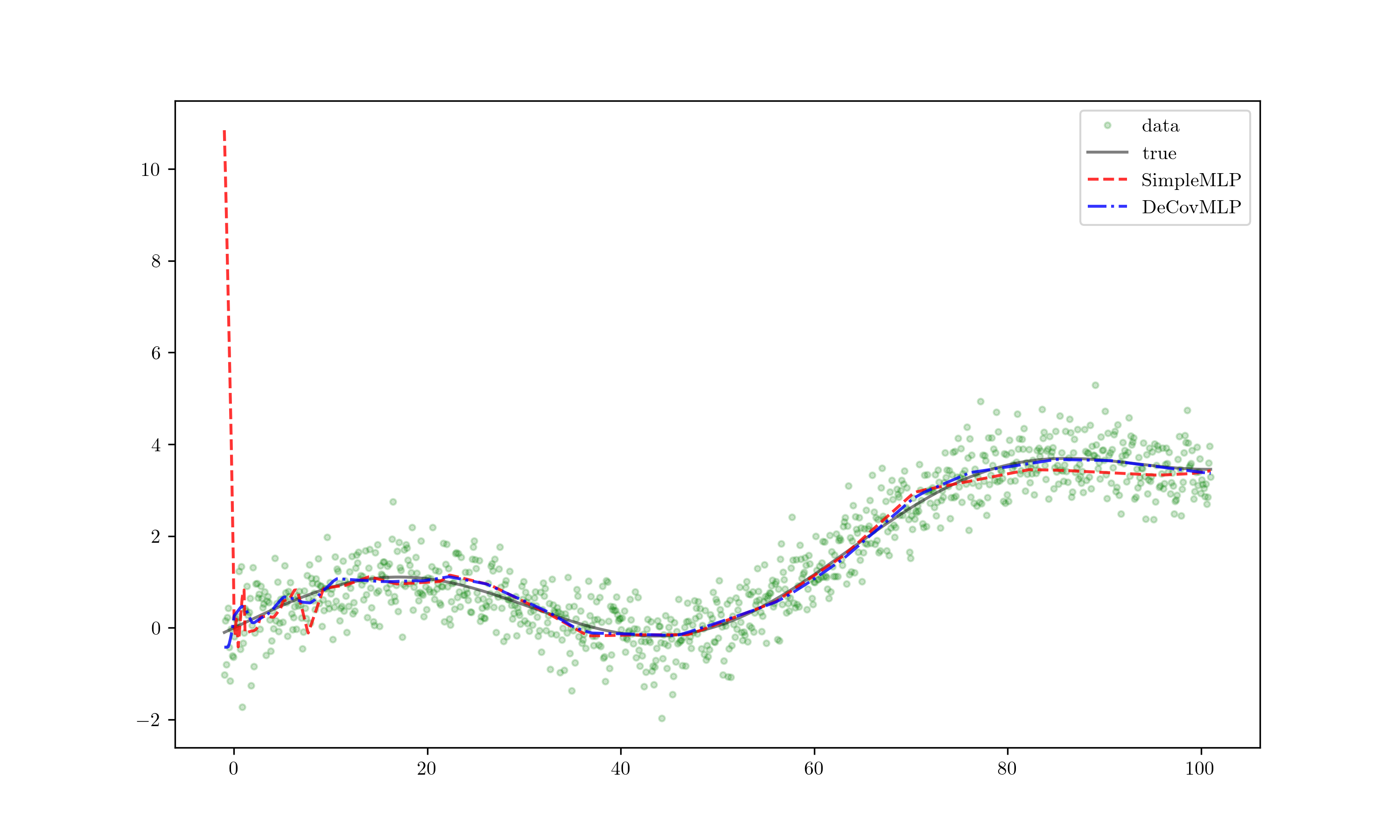
Extrapolate!
훈련 데이터셋에 과적합된 붉은 선은 정의역이 조금만 벗어나도 완전히 어긋난 결과를 보여주는 반면 푸른 선은 크게 벗어나지 않는 양상을 보여줍니다. 확실히 DeCovMLP가 더 일반화 성능이 뛰어나다는 것을 그림으로부터 알 수 있습니다.
4. Further more..
이 논문은 2015년에 발표된 논문으로 현재 2022년 기준으로 보면 상당히 오래된 논문입니다. 이후에도 Decorrelation에 대한 연구는 꾸준히 있어와서 최근에는 Decorrelated Batch Normalization 등 다양한 연구들이 발표되고 있습니다. 특히 Decorrelation은 과거부터 통계학에서 많이 다뤄져와서 이론적 근거와 분석이 탄탄하기에 신경망의 결과를 좀 더 직관적으로 이해할 수 있는 것 같습니다.
위 Regression 코드는 다음 링크에서 볼 수 있습니다.