5 분
🐪 가우시안 정복하기 01: 단일변수
물리학이나 통계학 등을 하다보면 항상 마주치는 원수 같은 존재가 있습니다. 별로 어렵지는 않은데 마주칠 때마다 헷갈리는 그 존재는 바로 가우스 적분(Gaussian Integral)입니다.
$$\int_{-\infty}^\infty e^{-\alpha x^2} dx$$
이공계 대학생이라면 1학년 미적분학 시간에 극좌표계(Polar coordinate)를 이용한 이중적분을 다룰 때 나오는 가장 기본문제로 가우스 적분을 기억할겁니다. 그러나 항상 거의 모두가 그렇듯이 시간이 지나면 지날 수록 기억은 풍화되고 거의 망각의 단계에 이르렀을 때에 갑자기 튀어나오는 낯선 형태의 가우스 적분들은 대처하기가 난감합니다.
따라서 여기서는 가우스 적분과 가우시안 분포에 대한 아주 기본적인 성질들을 다시 상기시키고 이를 발판삼아 다변수 가우시안(Multivariate Gaussian)과 여러 활용들을 살펴보도록 하겠습니다.
🔢 기본적인 가우스 적분
이해하기 위해 필요한 개념
- 고교 수준의 적분 (치환 적분, 지수함수의 적분)
- 극좌표계
- 이중적분
가우스 적분은 전형적인 처음 하기는 힘들지만 한 번 보면 누구나 할 수 있는 형태의 스킬입니다. 이것을 보고 극좌표계에서의 이중적분을 떠올리기는 힘들지만 그것을 사용한다는 것을 깨닫는 순간 문제는 아주 기초적인 미적분 문제로 격하됩니다. 그럼 먼저 가장 기본적인 가우스 적분을 봅시다.
일차원 가우스 적분
$$ \int_{-\infty}^\infty e^{-\alpha x^2} dx = \sqrt{\frac{\pi}{\alpha}} $$
이것을 바로 증명하기에는 어려움이 있으므로 제곱 꼴을 고려해야 합니다. $$\left(\int_{-\infty}^\infty e^{-\alpha x^2}\right)^2 = \int_{-\infty}^\infty \int_{-\infty}^\infty e^{-\alpha(x^2 + y^2)} dx dy$$ 이것을 $x^2 + y^2 = r^2,~dxdy = rdrd\theta$임을 이용하여 극좌표계 적분으로 변환합니다. 그렇다면 아주 간단한 치환 적분으로 적분을 계산할 수 있습니다. $$\int_{0}^\infty \int_{0}^{2\pi} re^{-\alpha r^2} dr d\theta = \frac{\pi}{\alpha}$$ 가우스 적분의 제곱이 위와 같은 결과가 되었고, 가우시안 함수($e^{-\alpha x^2}$)는 항상 양수이므로 위 식이 성립함을 알 수 있습니다.
보통 물리학이나 통계학에서 자주 사용되는 가우스 적분은 다음과 같은 형태입니다.
$$ \int_{-\infty}^\infty e^{-\frac{a}{2}y^2} dy = (2\pi)^{\frac{1}{2}} a^{-\frac{1}{2}} $$
일차원 가우스 적분 일반화
$$ (2\pi)^{-\frac{1}{2}}\int_{-\infty}^\infty e^{-\frac{1}{2}a x^2 + Jx} = a^{-\frac{1}{2}} e^{\frac{J^2}{2a}} $$
단순히 완전제곱식을 이용하여 정리하면 해결되는 적분입니다. $$\int_{-\infty}^\infty e^{-\frac{a}{2}(y - \frac{J}{a})^2 + \frac{J^2}{2a}} = \int_{-\infty}^\infty e^{-\frac{a}{2}t^2} dt \cdot e^{\frac{J^2}{2a}}$$
이런 형식의 적분은 평균이 0이 아닌 가우시안 분포나 양자 물리학의 경로 적분(Path Integral)에서 외부 힘(External force)이 작용할 때의 계산에서 많이 사용됩니다.
파인만 트릭을 이용한 가우스 적분
$$ \int_{-\infty}^\infty x^2 e^{-a x^2}dx = \frac{1}{2}\pi^{\frac{1}{2}} a^{-\frac{3}{2}} $$
먼저 다음과 같이 가우스 적분을 $a$에 대한 함수로 정의합니다. $$I(a) \equiv \int_{-\infty}^\infty e^{-ax^2} dx$$ 이를 $a$에 대해 편미분 합니다. $$\frac{\partial I(a)}{\partial a} = \int_{-\infty}^\infty -x^2 e^{-ax^2}dx$$ 우리는 이미 $I(a)$의 값이 $\sqrt{\pi}{a}$임을 알고 있습니다. 따라서 위 식에서 좌변의 값은 다음과 같습니다. $$\frac{\partial I(a)}{\partial a} = -\frac{1}{2}\pi^{\frac{1}{2}} a^{-\frac{3}{2}}$$ 이제 위 식 2개가 같음을 이용하면 증명은 끝납니다.
통상적으로 이런 적분은 부분적분(Partial integration)을 이용하는 것이 일반적이지만 파인만의 방법을 이용하면 이렇게 굉장히 쉽게 계산할 수 있습니다. 이런 트릭은 물리학에서는 일반적으로 사용되며 통계학에서도 아주 유용하게 사용할 수 있으므로 알아두면 큰 도움이 될 것입니다.
🐪 단변수 가우시안 (Single variate Gaussian)
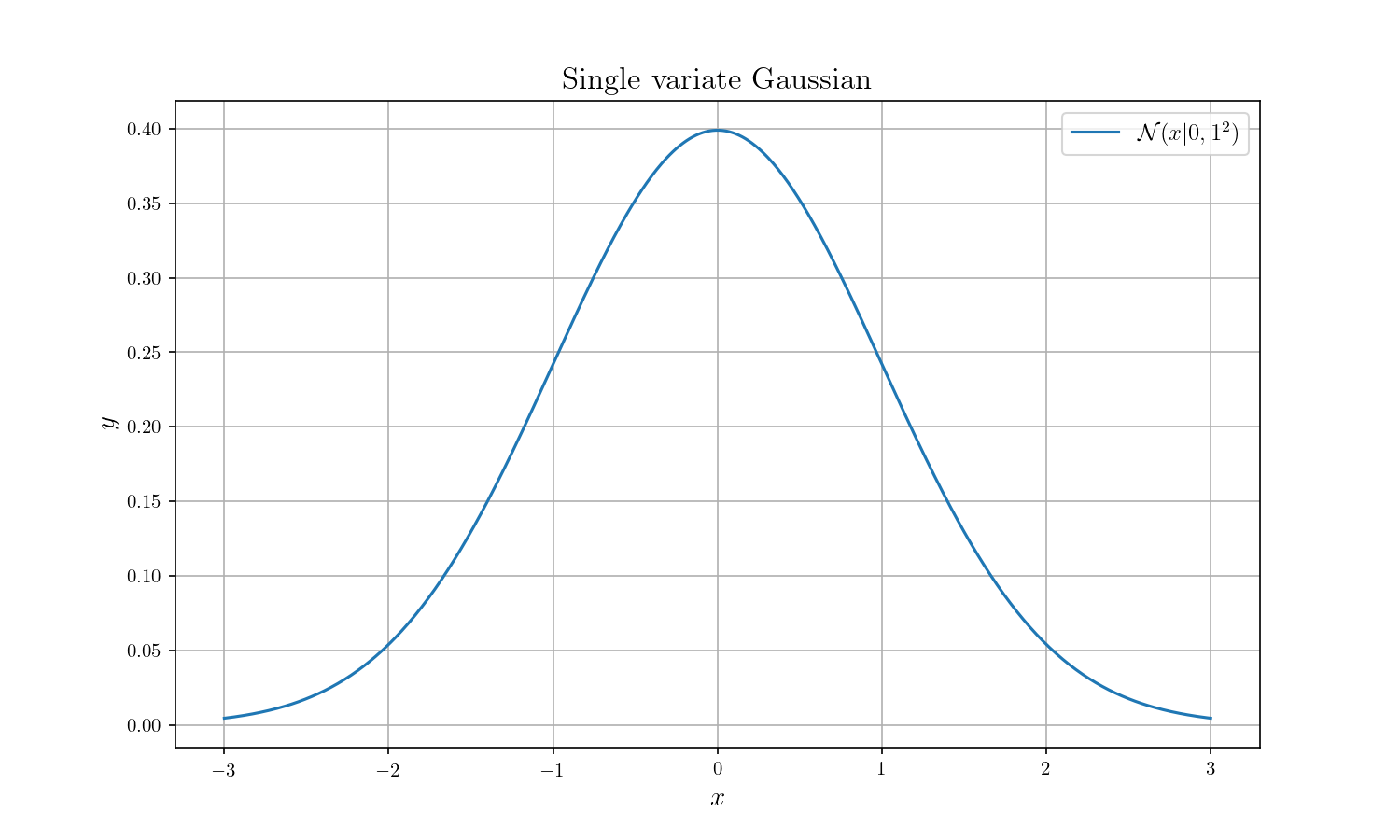
확률밀도함수 (Probability Density Function)
이해하기 위해 필요한 개념
- 고교 수준의 통계학
가우스 적분의 꽃은 역시 가우시안 분포라고 할 수 있습니다. 통계학에서 정규분포라고도 일컫는 이 확률 분포는 확률을 구하기 위해서 반드시 가우스 적분을 필요로 합니다. 단변수 가우시안 혹은 1차원 가우시안 분포의 확률밀도함수(Probability density function)은 다음과 같습니다.
$$ p(x) = \mathcal{N}(x | \mu, \sigma^2) = \frac{1}{\sqrt{2\pi \sigma^2}} \exp{\left(-\frac{1}{2\sigma^2}(x-\mu)^2 \right)} $$
위 식에서 보다시피 단변수 가우시안 분포를 정의하기 위해서는 두 매개변수(Parameter) $\mu$와 $\sigma$가 필요합니다. 이미 이 매개변수들의 의미를 알고 있는 사람들이 많을 것 같지만 일단은 매개변수 이상의 의미를 두지 않고 성질을 살펴보도록 하겠습니다.
위에서 확률밀도함수라고 미리 언급했지만, 징검다리도 두드려보고 건너 듯이 저 이상한 함수가 진짜 확률밀도함수인지 확인을 해봅시다. 확률밀도함수를 위시한 확률분포함수는 반드시 2가지의 조건을 충족해야 합니다.
-
정규화(Normalization) $$\int_{-\infty}^{\infty} p(x) dx = 1$$
-
음이 아닌 정부호(Nonnegative definite) $$p(x) \geq 0$$
위에서 정의한 가우시안 분포의 확률밀도함수는 지수함수 형태이므로 항상 0보다 큰 것은 자명합니다. 따라서 정규화 조건만 확인하면 징검다리가 안전함을 확인할 수 있습니다. 이미 눈치채셨을 수도 있겠지만 이 확률분포함수의 정규화 조건을 확인하는 것은 가우스 적분으로 해결할 수 있습니다.
$$ \int_{-\infty}^\infty \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left(-\frac{1}{2\sigma^2}(x - \mu)^2\right) dx = \frac{1}{\sqrt{2\pi\sigma^2}} \sqrt{2\pi \sigma^2} = 1 $$
모든 조건을 확인했으니 우리가 정의한 가우시안 분포의 확률밀도함수가 진짜라는 것을 납득할 수 있습니다. 이제 이 분포의 성질을 보기 위해 기댓값(평균)과 표준편차를 구해보도록 하겠습니다.
기댓값 (Expectation value)
확률밀도함수가 주어졌을 때, 기댓값의 정의는 다음과 같습니다.
$$ \mathbb{E}[X] = \int_{-\infty}^\infty x p(x) dx $$
이를 이용하여 단변수 가우시안 분포의 기댓값을 구해봅시다. 식이 조금 복잡할 수 있으니 상수는 제외하고 적분을 먼저 계산하겠습니다.
$$ \begin{align*} \int_{-\infty}^\infty xe^{-\frac{(x - \mu)^2}{2\sigma^2}} dx &= \int_{-\infty}^\infty (t + \mu) e^{-\frac{t^2}{2\sigma^2}} dt \\ &= \mu \sqrt{2\pi \sigma^2} \end{align*} $$
계산을 조금 설명하면, 첫 번째 줄에서는 단순히 $t=(x-\mu)$로 치환하여 전개하였고 이후, $t e^{-\frac{t^2}{2\sigma^2}}$이 기함수(Odd function)임을 이용, 적분 값이 0이 되므로 두번째 항만 가우스 적분을 이용하여 계산하였습니다. 이제 여기에 아까 잠깐 미뤄놓았던 상수를 곱해주면 다음과 같은 결과를 얻게 됩니다.
$$ \mathbb{E}[X] = \mu $$
놀랍게도 그저 매개변수 중 하나인 줄 알았던 $\mu$가 사실은 분포의 평균을 담당하는 중요한 변수였습니다! 이제 여세를 몰아 표준편차도 구해봅시다.
표준편차 (Standard deviation)
표준편차는 분산 (Variance) 을 구하면 자동으로 도출되는 값입니다. 분산의 정의는 다음과 같습니다.
$$ Var[X] = \mathbb{E}\left[(X - \mu)^2 \right] $$
그럼 바로 계산을 시작해봅시다.
$$ \begin{align*} \int_{-\infty}^\infty (x - \mu)^2 e^{-\frac{(x- \mu^2)}{2\sigma^2}} dx &= \int_{-\infty}^\infty t^2 e^{-\frac{t^2}{2\sigma^2}} dt \\ &= \frac{1}{2} \pi^{\frac{1}{2}} \left(\frac{1}{2\sigma^2}\right)^{-\frac{3}{2}} \\ &= \sigma^2 \sqrt{2\pi\sigma^2} \end{align*} $$
이번에는 앞서 다뤘던 파인만 트릭을 이용하여 계산했습니다. 기댓값을 구할 때와 마찬가지로 상수만 다시 붙여주면 다음과 같은 결과가 나옵니다.
$$ Var[X] = \sigma^2 $$
여기에 더 나아가, 표준편차는 분산의 양의 제곱근으로 정의되므로 $\sigma$가 바로 표준편차라는 것을 알 수 있습니다.
마치며
이번 글에서는 1차원 단일 변수에 대한 간단한 가우스 적분을 알아보고 이에 대한 활용으로 단변수 가우시안 분포의 기본적인 성질을 알아보았습니다. 다음에는 이를 다차원으로 확장하여 행렬 꼴로 표현되는 가우스 적분과 다변수 가우시안 분포에 대해 알아보겠습니다.
참고문헌
- Russell L. Herman, An introduction to Mathematical physics via oscillations, 2012
- Massimiliano Bonamente, Statistics and Analysis of Scientific Data, Springer, 2017