15 분
🏫 고등학교 수학으로 이해하는 선형회귀

세계에서 가장 유명하고 권위있는 과학저널인 사이언스(Science)에서는 매년 그 해의 가장 성공적이었다고 여겨지는 과학성과를 발표합니다. 2016년 12월 22일에도 2016 Breakthrough of the year 를 발표하면서 2016년에 있었던 과학 성과 중 가장 눈여겨봐야 할 10개의 과학성과를 발표했습니다. 순위는 다음과 같습니다.${}^{[1]}$
1. 중력파 발견
2. 외계행성 ‘프록시마b’ 발견
3. 인공지능 ‘알파고’와 이세돌 9단의 대결
4. 세포 노화 및 회춘 연구
5. 유인원의 마음 읽기 능력 연구
6. 단백질 구조설계 기술
7. 배아줄기세포로 만든 인공난자
8. 초기 인류의 확산 경로 연구
9. 휴대용 DNA 분석기
10. 초박막 메타렌즈 기술
2016년에는 중력파 관측이라는 엄청난 업적이 있었습니다. 이는 아인슈타인이 1916년 일반상대성이론을 발표한 지 정확히 100년이 되는 해에 이룬, 인류의 물리학 역사에 길이 남을 업적이었고, 실제로 중력파 관측에 지대한 공을 세운 세 명의 과학자는 1년만에 2017년 노벨 물리학상을 수상하였습니다. 그에 걸맞게 여러 매체에서도 동시에 보도하여, 과학에 관심있는 사람이라면 2016년을 중력파의 해로 기억하고 있을 겁니다.
하지만 여기서 말하고자 하는 것은 3번입니다. 아마도 대중에게는 1번보다 3번이 더 유명한 사건이었고, 특히 한국인들에게는 더더욱 잘 알려진 사건입니다. 중력파의 발견이 이후 천문학과 물리학의 새로운 연구방향을 제시했다면, 알파고의 바둑 정복은 이후 우리의 모든 삶에 머신러닝을 침투시키는 계기가 되었습니다. 이제는 어느 서비스에서나 머신러닝을 위시한 인공지능을 사용한다는 말이 들려오고, 대학들은 앞다투어 머신러닝 및 인공지능 관련 학과를 설치하고 있습니다. 이에 머신러닝을 공부해야겠다고 마음먹고 검색해보면, 여러 블로그에서 텐서플로우(Tensorflow), 파이토치(Pytorch), 케라스(Keras) 등으로 손글씨 인식하기 등의 머신러닝 응용에 대해서 다루는 것을 볼 수 있습니다. 하지만 왜 그렇게 되는 건지에 대해서 찾다보면 수 많은 논문들이 등장하며 여러 전문용어들이 쏟아져서 일반인들에게는 접근 자체가 어렵습니다. 따라서 이 게시물에서는 머신러닝의 가장 기본이 되는 MLE(Maximum Likelihood Estimation; 최대 가능도 추정) 에 대해 고등학교 수준의 수학 만 가지고 다뤄보려 합니다.
1. 데이터의 확률화
이해하기 위해 필요한 개념
- 고교 교과과정 - 확률과 통계
1.1. 기본 표기법
MLE를 시작하기에 앞서 고등학교때 배운 확률과 통계를 이용하여 데이터를 표현하는 것부터 연습하겠습니다. 표기 방식은 아주 유명한 머신러닝 책인 Bishop의 PRML(Pattern Recognition and Machine Learning; 패턴인식과 머신러닝)에서 사용하는 표기법 을 사용하겠습니다. 대부분 고등학교 표기방식과 동일합니다만, 조금의 차이가 있습니다. 저희가 사용할 표기법은 다음과 같습니다.
| 개념 | 표기법 | 고교 표기 |
|---|---|---|
| 단일 스칼라 확률변수 | $x \in \mathbb{R}$ | 집합 $X$ |
| 확률분포함수 | $p(x) \geq 0$ | $P(X=x) \geq 0$ |
| 결합확률분포 | $p(x,y)$ | – |
| 조건부확률분포 | $p(x | y)$ | – |
| 균등분포 | $\text{Unif}(x|a,b)$ | – |
| 이항분포 | $\text{Bin}(x|N, \mu)$ | $B(n, p)$ |
| 정규분포 | $\mathcal{N}(x|\mu,\sigma^2)$ | $N(m,\sigma^2)$ |
위에서 보면 알겠지만, 고등학교에서 다룬 확률분포함수는 오로지 단일 확률분포일뿐, 결합이나 조건부 등의 변수가 2개 이상인 확률분포함수는 다루지 않았습니다. 다만, 그에 상응하는 확률인 곱사건의 확률($P(A\cap B)$이나 조건부확률($P(A|B)$) 자체는 다루었으니 비슷한 맥락으로 접근하면 쉽게 이해할 수 있습니다. 예를 들어, 조건부확률분포와 결합확률분포 사이에는 다음의 관계식이 성립합니다.
$$ p(x|y) = \frac{p(x,y)}{p(y)} $$
이는 고등학교에서 다루었던 조건부확률의 정의와 부합합니다.
$$ P(X | Y) = \frac{P(X\cap Y)}{P(Y)} $$
이쯤에서 헷갈리기 시작합니다. 도대체, 확률분포와 확률의 차이는 뭘까요?
1.2. 확률 vs 확률분포
다음 고등학교 문제를 봅시다.
Q. 주사위를 720번 던져서 1의 눈이 140번 이상 나올 확률은 얼마인가?
이 문제는 큰 수의 법칙을 다루는 전형적인 문제로 이항분포에서 평균과 표준편차를 구한 후 정규분포로 근사하여 푸는 문제입니다. 이 문제를 푸는 방법은 다음과 같습니다.
주사위의 1의 눈이 나오는 횟수를 확률변수 $X$라 두자. 이때, 주사위를 던지는 것은 모두 독립시행이므로 이 확률변수는 이항분포를 따르게 된다. $$p(x) = \text{Bin}(x | 720,\frac{1}{6})$$ 이항분포 $\text{Bin}(x | n,p)$의 평균은 $np$이며 분산은 $npq$이므로, 평균은 $120$, 표준편차는 $10$이다. 이때, $720$은 충분히 큰 수이므로 확률분포가 다음의 정규분포를 따른다고 근사할 수 있다. $$p(x) \simeq \mathcal{N}(x | 120, 10^2)$$ 이때, 140번 이상 나올 확률을 나타내고, 표준화하는 과정은 다음과 같다. $$p(x \geq 300) = p(z \geq \frac{140 - 120}{10}) = p(z \geq 2)$$ 이를 표준정규분포표로 계산하면 $0.0228$이 나온다.
언뜻보면 위 문제는 720번의 시행이 전제되어있으므로 데이터를 다루는 것처럼 보입니다. 그리고 문제를 풀때에는 오로지 단일 확률변수만 사용하고 있습니다. 고교에서는 이런 문제들만 다루기에 데이터를 다루는데에 여러가지 확률변수가 필요하다는 것을 이해하기가 어렵습니다. 하지만, 위 문제는 전혀 데이터를 다룬 문제가 아닙니다. 오로지 정규분포에 근거한 수학적 확률을 묻는 문제일 뿐입니다. 실제 데이터를 다룬 이항분포 문제는 다음과 같습니다.
Q. 주사위를 120번 던지는 시행을 6번 반복하여 1의 눈이 나온 데이터는 다음과 같다.
시행 1 2 3 4 5 6 횟수 10 23 18 15 26 21 이를 이용하여 주사위를 720번 던졌을 때, 1의 눈이 140번 이상 나올 확률을 계산하시오.
문제가 사뭇 달라졌습니다. 앞서서 풀었던 고교문제는 오로지 수학적 확률을 가정하여 주사위의 1의 눈이 나올 확률은 $1/6$으로 고정하고 이항분포로 풀었지만, 여기서는 실제 데이터로 이항분포를 추정하여 풀어야 합니다. 추정과정은 다음과 같습니다.
- 각 시행 횟수를 확률변수 $x_1,,x_2,,\cdots,,x_6$으로 둔다.
- 각 확률변수들은 모두 독립이라 가정하며 동일한 이항분포 $\text{Bin}(120,p)$를 따른다고 가정한다.
- 최대가능도추정이나 베이즈 추론을 이용하여 $p$를 추정한다.
여기서는 3번에서 최대가능도추정을 이용할텐데, 아직 최대가능도추정을 배우지 않았으니, 계산결과만 명시하면 $p$는 $113/720$이라는 결과가 나옵니다. 이를 이용하여 계산하면 평균과 분산이 이전과 달라집니다. 평균은 $113$으로 주어지고, 표준편차는 약 $9.76$정도로 주어집니다. 따라서 확률을 계산하면 다음과 같습니다.
$$ p(x \geq 140) = p(z \geq \frac{140 - 113}{9.76}) \simeq p(z \geq 2.77) \simeq 0.0028 $$
앞선 결과와 거의 10배에 해당하는 차이를 보입니다. 데이터가 6개 밖에 되지 않아 충분하지 않았기 때문입니다. 실제로 데이터를 10000개 정도로 늘린 후에 계산한 확률은 $0.0220$정도로 수학적 확률과 좀 더 비슷한 결과를 보입니다. 이 과정을 Julia 코드로 나타내면 다음과 같습니다.
# https://github.com/Axect/Blog_Code
using Distributions
b = Binomial(120, 1/6); # 이항분포 선언
x = rand(b, 10000); # 데이터 추출
y = x ./ 120; # 확률로 변환
p = mean(y); # 최대가능도추정으로 구한 p
b2 = Binomial(720, p); # 구한 이항분포
m = mean(b2); # 평균
σ = std(b2); # 표준편차
t = (140 - m) / σ # 140의 표준화
n = Normal(0,1) # 표준정규분포
result = 1 - cdf(n, t) # 결과
@show result # 결과 출력
그럼 이제 본격적으로 데이터의 확률분포에 대해서 다뤄봅시다.
1.3. 데이터의 확률분포
앞서 봤다시피, 데이터는 여러 개의 확률변수들의 집합으로 나타낼 수 있습니다.
$$ \mathcal{D} = \left\{x_1,\,x_2,\,\cdots,\,x_n\right\} $$
실제로 다룰때에는 집합보다는 벡터로 다루는 것이 더 효율적이므로 다음과 같이 벡터로 표기할 수 있습니다. (세로로 표기한 이유는 많은 수치 프로그램에서 열벡터 형식을 사용하기 때문인데, 그냥 벡터를 세로로 표기했다고 생각하면 됩니다.)
$$ \mathbf{x} = \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix} $$
일단, 여기서는 이해를 쉽게 하기 위하여 집합으로 설명하겠습니다. 데이터의 확률분포는 다음과 같이 여러 확률변수들의 결합분포로 나타낼 수 있습니다.
$$ p(\mathcal{D}) = p(x_1,\,x_2,\,\cdots,\,x_n) $$
일반적인 경우에는 여러 임의의 확률변수들의 결합분포를 나타내는 것은 매우 어려운 일이므로 저희는 데이터에 아주 강력한 전제조건을 부여할 겁니다. 바로, i.i.d.(independent and identically distributed; 독립항등분포) 입니다.
i.i.d는 모든 확률변수들이 독립이며, 동일한 분포를 따른다는 가정으로 굉장히 강력한 가정이지만 의외로 자연에서 볼 수 있는 대부분의 데이터에 대해서는 큰 문제가 없는 가정입니다. i.i.d를 가정하면 데이터의 확률분포를 아주 많이 개선시킬 수 있습니다.
$$ p(\mathcal{D}) = p(x_1)\times p(x_2)\times \cdots \times p(x_n) = \prod_{i=1}^n p(x_i) $$
마지막에 있는 원주율 $\pi$의 대문자인 $\Pi$는 $i=1$부터 $i=n$까지의 곱을 의미합니다. 이제 저 확률변수들이 어떤 분포를 가지는지 알면 그의 곱으로 데이터의 확률분포를 표현할 수 있습니다.
2. 전체 확률의 법칙과 베이즈 정리
이해하기 위해 필요한 개념
- 고교 교과과정 - 확률과 통계
지금까지 데이터를 확률화하는 방법에 대해 알아보았으니, 이제 임의의 데이터를 어떻게 선형으로 근사할 수 있을지에 대해 알아보려합니다. 그러기 위해서는 반드시 알아야할 두 가지 중요한 확률 법칙이 있는데, 전체 확률의 법칙(전확률 정리)과 베이즈 정리 입니다.
2.1. 파티션 (Partition)
전체 확률의 법칙과 베이즈 정리에는 중요한 전제조건이 있는데, 바로 파티션(Partition) 을 찾아야 한다는 것입니다. 파티션이라는 이름은 들어보신 분도 있을 텐데, 아마 제일 잘 알려진 파티션은 아래 사진일 겁니다.

회사 칸막이 (출처: PIXNIO)
그 외에도 디스크 파티션이나 공간을 분할하는 장식장 역할을 하는 파티션 등 여러 파티션들이 있는데, 이들은 모두 공통적인 성질을 가집니다. 바로, 어떤 것을 분리하여 나눈다는 것입니다. 통계에서의 파티션은 표본 공간을 전부 겹치지 않게 분할하는 사건들의 집합을 의미합니다. 아래 그림에서는 $A_1,\,A_2,\,A_3,\,A_4$가 $S$의 파티션입니다.
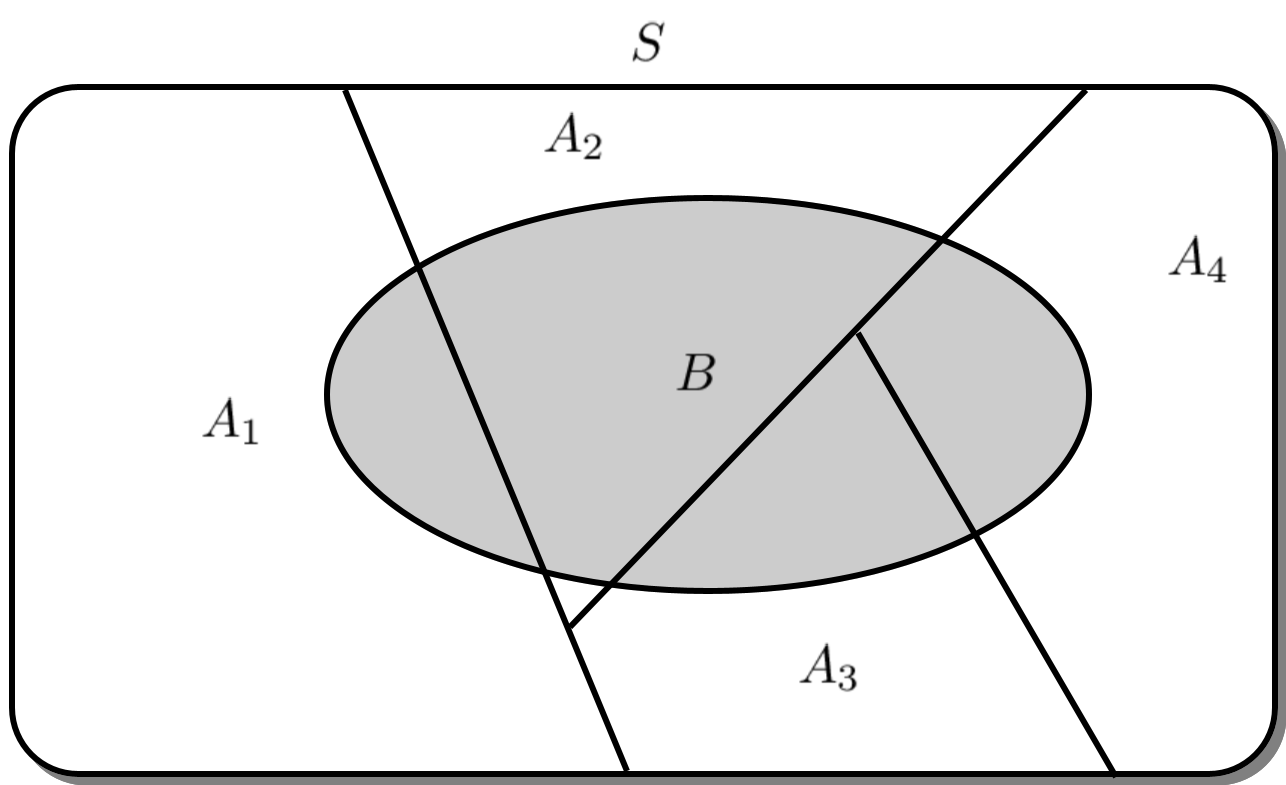
통계에서의 파티션
이를 수학적으로 표현하면 다음과 같습니다.
파티션
표본 공간 $S$ 에 대하여 그 부분집합들의 수열 $\left\{A_i \right\}_{i=1}^n$이 다음 성질들을 만족하면 $S$의 파티션(Partition)이라 부른다.
- $A_i \cap A_j = \emptyset \quad (i,j=1,2,\cdots,n)$
- $A_1 \cup A_2 \cdots \cup A_n = S$
2.2. 전체 확률의 법칙
전체 확률의 법칙은, 용어는 어려워보이지만 사실 아주 간단한 법칙입니다. 위 파티션 그림을 보면 $S$의 부분집합 $B$는 다음과 같이 표현할 수 있습니다.
$$ B = (A_1 \cap B) \cup (A_2 \cap B) \cup (A_3 \cap B) \cup (A_4 \cap B) $$
이때, $A_1,A_2,A_3,A_4$는 모두 파티션이므로 교집합이 공집합이며 따라서 사건 $B$의 확률은 다음과 같이 나타낼 수 있습니다.
$$ p(B) = \sum_{i=1}^4 p(A_i \cap B) $$
이를 확률의 곱셈정리를 이용하여 나타내면 다음과 같습니다.
$$ p(B) = \sum_{i=1}^4 p(A_i \cap B) = \sum_{i=1}^4 p(B | A_i)p(A_i) $$
이것이 전체 확률의 법칙입니다. 즉, 요약하면 전체 확률의 법칙은 어떤 파티션이 정의된다면, 임의의 사건에 대해서 그 사건이 일어날 확률을 파티션과의 결합 확률의 합으로 나타낼 수 있다는 것입니다. 수학적으로 정의하면 다음과 같습니다.
전체 확률의 법칙
표본 공간 $S$에 대해, $\left\{A_i\right\}_{i=1}^n$이 $S$의 파티션이라면 임의의 사건 $B\subset S$의 확률은 항상 다음과 같이 나타낼 수 있다.
$$ p(B) = \sum_{i=1}^n p(A_i \cap B) = \sum_{i=1}^n p(B | A_i)p(A_i) $$
전체 확률의 법칙은 실제로 고등학교 문제에도 자주 쓰입니다. 다음 문제를 봅시다.
Q. 깃헙고등학교는 1학년 20%, 2학년 40%, 3학년 40%로 이루어져 있다. 1학년 중 남학생의 비율은 40%, 2학년 중 남학생의 비율은 50%, 3학년 중 남학생의 비율은 60%라면, 전체 남학생의 비율은 얼마인가?
조건부 확률의 굉장히 전형적인 문제로, 쉽게 풀리는 문제입니다. 풀이는 다음과 같습니다.
고1, 고2, 고3은 상호 배타적이고 모두 합치면 전체가 되므로 파티션의 성질을 만족한다. 이를 $A_1,\,A_2,\,A_3$라 하고, 남학생일 사건을 $B$라고 하자. 그렇다면 전체 확률의 법칙에 의해 남학생의 비율은 다음과 같다. $$ \begin{aligned} p(B) &= p(A_1 \cap B) + p(A_2\cap B) + p(A_3 \cap B) \\ &= p(B|A_1)p(A_1) + p(B|A_2)p(A_2) + p(B|A_3)p(A_3) \\ &= 0.4 \times 0.2 + 0.5 \times 0.4 + 0.6 \times 0.4 = 0.52 \end{aligned} $$
2.3. 베이즈 정리
베이즈 정리는 전체 확률의 법칙의 다음 단계로 볼 수 있습니다. 위 문제에서 봤다시피, 보통 우리는 파티션을 전제했을 때, 다른 사건의 확률이나 비율($p(B|A_i)$)의 정보를 갖고 다른 확률을 계산합니다. 전체 확률의 법칙은 해당 사건의 확률($p(B)$)을 구하려는 것이었다면, 베이즈 정리는 반대로 해당 사건을 전제하였을 때의 파티션의 확률($p(A_i|B)$)을 구하는 것이 목적입니다. 이는 조건부 확률의 정의와 전체확률의 법칙을 이용하면 간단히 구할 수 있습니다.
$$ p(A_i | B) = \frac{p(A_i \cap B)}{p(B)} = \frac{p(B|A_i)p(A_i)}{\displaystyle \sum_{j=1}^n p(B|A_j)p(A_j)} $$
좀 더 수학적으로 정의하면 다음과 같습니다.
베이즈 정리
표본 공간 $S$에 대해, $\{A_i\}_{i=1}^n$이 $S$의 파티션이라면 임의의 사건 $B \subset S$에 대해 다음의 등식이 성립한다.
$$ p(A_i|B) = \frac{p(B|A_i) p(A_i)}{\displaystyle \sum_{j=1}^n p(B|A_j)p(A_j)} $$
베이즈 정리의 진가는 데이터와 결부되었을 때 나타납니다. $\{C_i\}_{i=1}^n$가 파티션이고, 데이터가 $\mathcal{D}$로 주어졌을 때, 이에 대한 베이즈 정리를 쓰면 다음과 같습니다.
$$ p(C_i | \mathcal{D}) \propto p(\mathcal{D} | C_i)p(C_i) $$
이때, 분모를 생략한 까닭은 좌변은 $C_i$에 대한 확률인데, 분모는 $p(\mathcal{D})$이므로 $C_i$에 대한 의존성이 없습니다. 따라서 단순 상수 취급을 하여 위 비례식을 적을 수 있습니다. 위 식의 항들은 보통 다음과 같이 해석됩니다.
- $C_i$ : $i$번째 모델(범주)
- $\mathcal{D}$ : 데이터
- $p(C_i)$ : 모델의 사전 확률 (Prior probability)
- $p(\mathcal{D} | C_i)$ : 가능도 (Likelihood)
- $p(C_i | \mathcal{D})$ : 사후 확률 (Posterior probability)
낯선 용어들이 많아 헷갈릴 수 있는데, 고양이와 개의 사진을 구분하는 작업을 예로 들어봅시다.
- $C_1$ = 개, $C_2$ = 고양이
- $\mathcal{D}$ : 개나 고양이 혹은 다른 것들이 섞인 사진들
- $p(C_i)$ : 테스트 데이터들의 개, 고양이 사진 비율에 대한 사전 지식
- $p(\mathcal{D} | C_i)$ : 개나 고양이를 전제했을 때의 데이터의 확률 분포 (개나 고양이일 가능성)
- $p(C_i | \mathcal{D})$ : 데이터가 개나 고양이일 확률
위 예를 보면 알겠지만, 우리의 최종 목표는 사후 확률을 구하는 것입니다. 즉, 어떤 데이터를 보고 그 데이터가 어떤 범주에 속할 지 분류하거나 혹은 확률분포에 필요한 매개변수를 추정하는 것이 목표이죠. 위에서는 분류로 예를 들었지만, 여기서 해볼 것은 매개변수의 추정입니다.
3. 선형회귀
이해하기 위해 필요한 개념
- 고교 교과과정 - 미적분
- 고교 교과과정 - 확률과 통계
3.1 노이즈 (Noise)
이번에도 고등학교 확률과 통계 문제로 예를 들면서 시작해봅시다.
Q. 어느 반의 수학성적이 평균이 60, 표준편차가 20인 정규분포를 따른다고 할 때, 1등급이 나오기 위해서는 최소 몇 점 이상을 받아야 하는가? (단, $p(0 \leq Z \leq 1.75)=0.46$)
풀이는 다음과 같습니다.
1등급이 나오기 위한 최소 점수를 $a$라 하자. 그렇다면 다음 등식을 만족해야 한다. $$ p(X \geq a) = 0.04 $$ 이를 표준화하면 다음과 같다. $$ p(X \geq a) = p(Z \geq \frac{a - 60}{20}) = 0.04 = p(Z \geq 1.75) $$ 따라서 $a=95$이다.
문제는 쉬웠지만, 이것이 실제로 가능한 문제일까요? 만일, 본인 반의 평균과 표준편차를 알고 있다면 본인의 등급을 추정할 수 있을까요? 결론부터 말하자면, 불가능합니다. 이유는 수학 성적이 아무리 정규분포와 비슷하게 나오더라도 정확히 정규분포일 확률은 아주 작기 때문입니다.
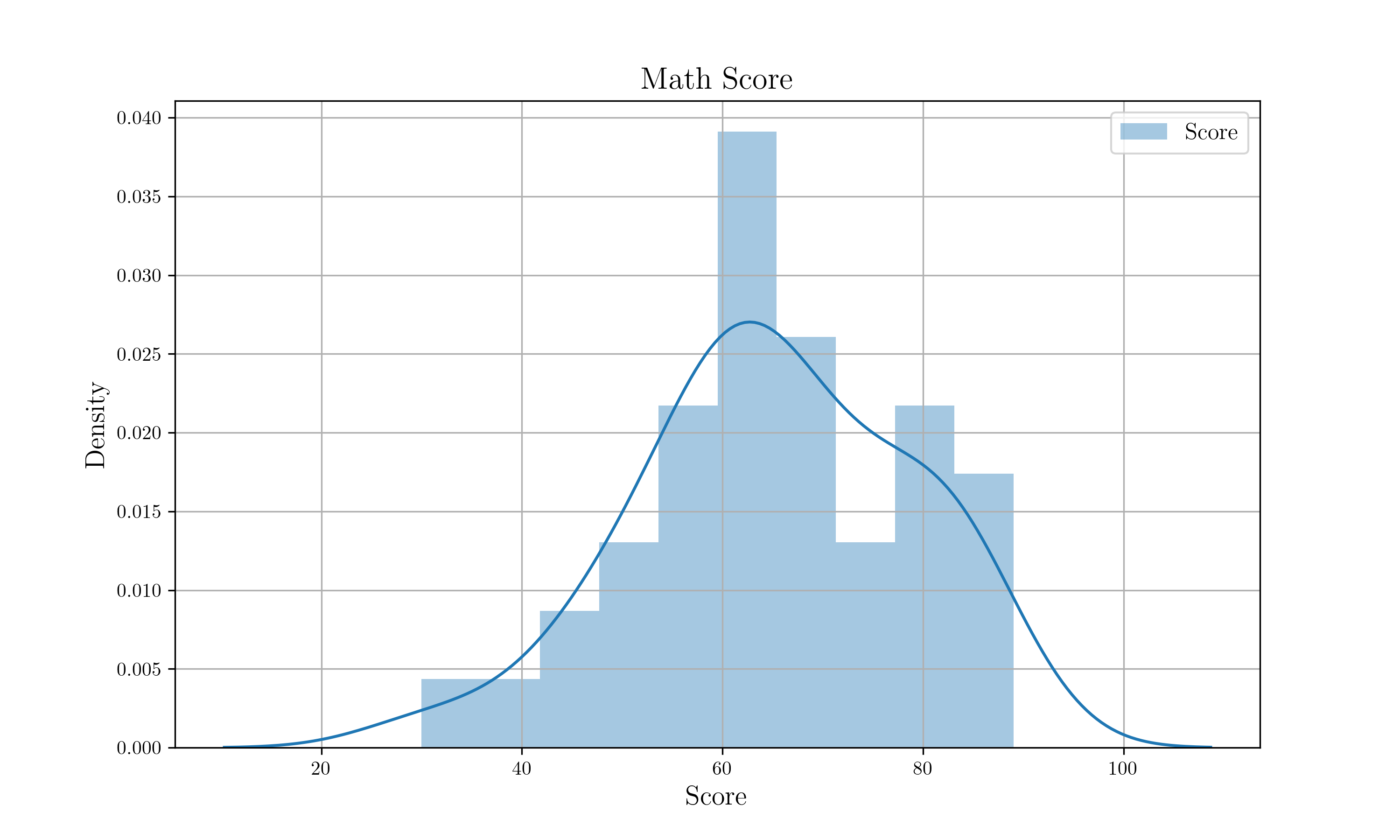
정확히 정규분포인 성적은 잘 나오지 않습니다.
실제로 표본이 엄청나게 많은 수능 성적조차 정확히 정규분포를 따르지 않습니다. 위 문제처럼 등급컷을 추론해보아도 실제 등급컷과는 괴리를 보이죠. 2019년 11월 14일에 치뤄진 2020년 수능 국어에 대한 데이터는 다음과 같았습니다.${}^{[2]}$
| 시험 | 과목 | 평균 | 표준편차 | 1등급 컷 |
|---|---|---|---|---|
| 2020 수능 | 국어 | 59.87 | 20.22 | 91 |
이를 정규분포로 바꾸어 91점 이상인 학생들의 비율을 계산하면 $0.062$, 즉, 6.2%가 나옵니다. 95점 이상인 학생들의 비율을 계산해야 비로소 $0.0412$ 정도로 나오므로 만일, 2020 수능 국어가 정규분포를 따랐다면 95점이 1등급 컷 점수였어야 합니다. 사실 수능까지도 갈 필요가 없고 주사위를 던져서 1의 눈의 수를 확인한다고 해봐도 정확히 이항분포를 따르지 않는 것을 볼 수 있습니다. 이렇게 통계학에서는 실제 값과 이론 값은 딱히 다른 요인이 없어도 차이를 보이게 되는데, 이때의 차이를 노이즈(Noise) 라고 부릅니다.
노이즈는 관측 기기나 실험에서 일어나는 오류와는 다르게, 자연에 항상 존재하는 것으로 더 정밀하게 측정하거나 실험 기법을 바꾼다고 해서 줄어들지 않습니다. 휴대폰 카메라 대신 더 화질 좋은 DSLR을 들고 온다 해도 관측한 1의 눈이 나온 횟수는 바뀌지 않죠.
자연에서 발생하는 노이즈의 확률분포는 많은 경우에 정규분포를 따릅니다. 여러 분포들이 표본이 커지게 되면 정규분포로 근사되는 것과 정규분포 자체가 실험오차를 분석하는 것에서 유래했다는 것을 생각해보면 어느 정도 납득이 될 겁니다. 따라서 이 게시물에서 다룰 노이즈들은 모두 정규분포를 따른다고 가정할 것입니다.
3.2. 선형 모델
우리는 선형회귀를 하는 것이 목적이기에 $(x,y)$ 순서쌍으로 표기된 데이터가 주어졌을 때, 다음과 같은 관계식을 기대합니다.
$$ y = ax + b $$
예를 들어, 데이터가 $(1,3), (2,5), (3,7)$로 주어졌으면, 관계식은 $y=2x+1$이 됩니다. 하지만, 앞서 말했듯이 모든 데이터에는 노이즈가 존재합니다. 보통 다음과 같은 데이터가 주어진다고 보면 됩니다.
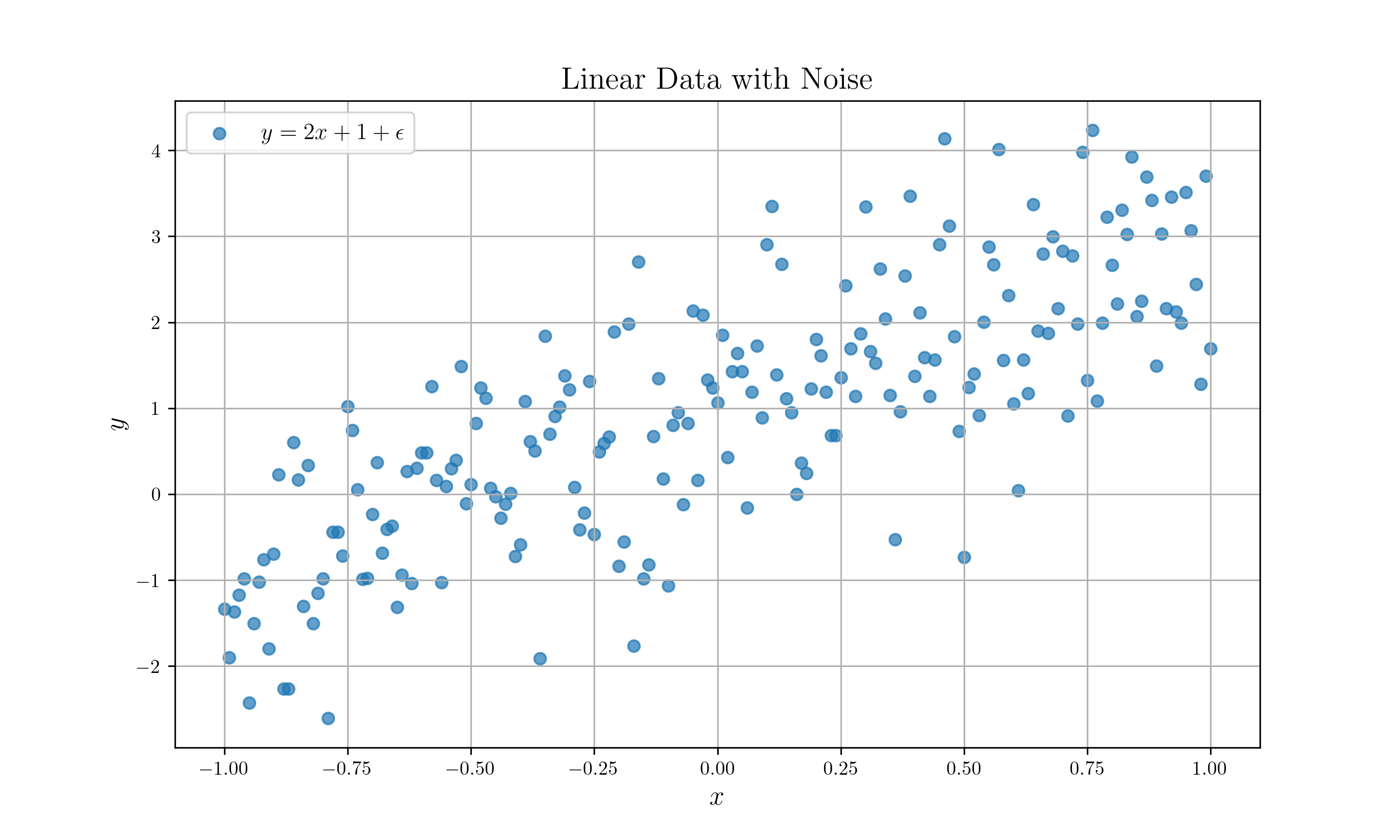
$y=2x+1$에 노이즈를 더한 데이터
즉, 다시 관계식을 나타내면 다음과 같습니다.
$$ y = ax + b + \epsilon $$
여기서 중요한 것은 $\epsilon$은 확률변수라는 것입니다. 앞서 언급한대로 $\epsilon$의 확률분포는 정규분포로 가정할 것입니다. 노이즈의 평균은 당연하게도 $0$일 것이므로 이를 서술하면 다음과 같습니다.
$$ p(\epsilon) = \mathcal{N}(\epsilon | 0, \sigma^2) $$
$a,b$는 아직 결정되지는 않았지만, 상수일 것이고 $x$는 단순히 입력값으로 간주할 것이므로 확률변수로 취급하지 않을 것입니다. 따라서 $y$는 다음의 확률분포를 따르게 됩니다.
$$ p(y) = \mathcal{N}(y| ax+b, \sigma^2) $$
3.3 최대 가능도 추정 (MLE)
앞서 베이즈 정리 단원에서 언급했다시피, 우리의 목적은 주어진 데이터들의 분포로부터 사후확률분포를 구하는 것입니다. 이를 추정하는 방법은 크게 두 가지로 나눠집니다.
- 최대 가능도 추정 (Maximum Likelihood Estimation)
- 베이즈 추론 (Bayesian Inference)
여기서는 1번의 방법을 따라 설명하겠습니다. 앞서 본 것처럼, 베이즈 정리를 이용하면 사후확률분포의 비례식을 작성할 수 있습니다.
$$ p(C_i | \mathcal{D}) \propto p(\mathcal{D} | C_i)p(C_i) $$
이때, $p(C_i)$는 데이터와 상관없는 사전확률분포이므로 $p(\mathcal{D}|C_i)$를 최대화하면 $p(C_i|\mathcal{D})$ 역시 최대가 되지 않겠냐는 것이 최대 가능도 추정입니다. 따라서 이 경우엔 사후확률분포함수는 구할 수 없고 단순히 사후확률분포가 최대가 되는 지점만 구할 수 있습니다. 이에 대해서는 장단점이 있는데, 간단한 선형회귀에서는 이것으로도 충분합니다.
앞서 세운 선형모델을 베이즈 정리로 적어보면, 가능도(likelihood)는 다음과 같습니다.
$$ p(\mathcal{D}|a,b) = p(\mathbf{y}|\mathbf{x},a,b)p(\mathbf{x}) = \left\{ \prod_{i=1}^n\mathcal{N}(y_i|ax_i+b,\sigma^2)\right\} \times p(\mathbf{x}) $$
위 식에서 $\mathbf{x},~ \mathbf{y}$는 각각 $(x_1,\cdots,x_n),~(y_1,\cdots,y_n)$을 나타냅니다. 이제 이것을 최대로 만드는 $a,~b$를 찾기만 하면 되는데, 이는 고등학교 미적분 문제처럼 접근하면 됩니다. 극대, 극소를 먼저 찾고, 그것이 최대인지 최소인지 구분하면 되는 것이죠. 다만, 위 식처럼 $n$개의 곱으로 되어있는 경우에는 미분하기가 힘드므로 먼저 로그를 취한 후 미분하도록 하겠습니다.
$$ \begin{aligned} \ln p(\mathcal{D}|a,b) &= \sum_{i=1}^n \ln \left\{\mathcal{N}(y_i|ax_i + b, \sigma^2)\right\} + \ln p(\mathbf{x}) \\ &= \sum_{i=1}^n \left\{- \ln(\sqrt{2\pi\sigma^2}) - \frac{(y_i - (ax_i+b))^2}{2\sigma^2} \right\} + \ln p(\mathbf{x}) \end{aligned} $$
곱이 합으로 바뀌었습니다. 이제 이를 $a,b$로 각각 미분하여 0이 되는 값을 구해볼 겁니다. 이때, 두 번째줄의 첫 항과 마지막 항은 $a,b$와 상관없으니 무시하고 계산합시다.
1) $b$로 미분
$$ \begin{aligned} &\frac{\partial}{\partial b} \ln p(\mathcal{D}|a,b) = -\frac{1}{\sigma^2}\sum_{i=1}^n (y_i - ax_i - b) = 0 \\ \Rightarrow~&\therefore b = \overline{y} - a\overline{x} \qquad (\overline{x} \equiv \frac{1}{n}\sum_{i=1}^n x_i,~\overline{y} = \frac{1}{n}\sum_{i=1}^n y_i) \end{aligned} $$
2) $a$로 미분
$$ \begin{aligned} &\frac{\partial}{\partial a} \ln p(\mathcal{D}|a,b) = -\frac{1}{\sigma^2}\sum_{i=1}^n (ax_i + b - y_i) x_i = 0 \\ \Rightarrow~& a \sum_{i=1}^n x_i^2 + b \sum_{i=1}^n x_i - \sum_{i=1}^n x_iy_i = 0 \\ \Rightarrow~& a\overline{x^2} - (a\overline{x} - \overline{y}) \overline{x} - \overline{xy} = 0 \\ \\ \Rightarrow~&\therefore a = \frac{\overline{xy} - \overline{x}\overline{y}}{\overline{x^2} - \overline{x}^2} \end{aligned} $$
위 결과를 요약하면 다음과 같습니다.
선형모델의 최대 가능도 추정
데이터 $\mathcal{D} = \left\{(x_1,y_1),\,\cdots,\, (x_n,y_n)\right\}$으로 주어졌을때, 이를 최대 가능도 추정을 통해 선형모델 $y=ax+b+\epsilon$로 근사한다면 이에 대한 매개변수 $a,b$는 다음과 같이 구할 수 있다.
$$ a = \frac{\overline{xy} - \overline{x}\overline{y}}{\overline{x^2} - \overline{x}^2},\quad b = \overline{y} - a\overline{x} $$
이제 이를 코드로 나타내봅시다.
3.4. 코드 구현
코드는 편의를 위해 Julia를 이용하겠습니다. 다음 코드를 위해 필요한 것은 다음과 같습니다.
Pre-requisites
- Julia
- NCDataFrame
- Statistics
- DataFrames
- Python
- NetCDF4
- matplotlib
- libnetcdf
필요한 데이터는 위에서 선형 모델을 설명하기 위해 추출하였던 데이터를 사용하겠습니다. 데이터 추출 코드는 부록에 수록해놓았습니다.
# Julia
# https://git.io/Jm2gf
using NCDataFrame, Statistics, DataFrames
# 데이터 불러오기
df = readnc("linear.nc")
# 표본평균 구하기
x_bar = mean(df[!,:x])
y_bar = mean(df[!,:y])
x²_bar = mean(df[!,:x] .^ 2)
xy_bar = mean(df[!,:x] .* df[!,:y])
# 최대가능도추정
a = (xy_bar - x_bar * y_bar) / (x²_bar - x_bar^2)
b = y_bar - a * x_bar
# a,b 출력
@show a
@show b
# 그림 그릴 준비
x_plot = -1.0:0.01:1.0
y_plot = a .* x_plot .+ b
# 데이터 쓰기
dg = DataFrame(x=x_plot, y=y_plot)
writenc(dg, "linear_plot.nc")
이렇게 나온 데이터를 갖고 그림을 그리는 코드는 다음과 같습니다.
# Python
# https://git.io/Jm2gs
from netCDF4 import Dataset
import matplotlib.pyplot as plt
# Import netCDF file
ncfile = './linear.nc'
data = Dataset(ncfile)
var = data.variables
# Prepare Data to Plot
x = var['x'][:]
y = var['y'][:]
# Import netCDF file
ncfile = './linear_plot.nc'
data = Dataset(ncfile)
var = data.variables
# Prepare Data to Plot
x_reg = var['x'][:]
y_reg = var['y'][:]
a = var['a'][:][0]
b = var['b'][:][0]
# Use latex
plt.rc('text', usetex=True)
plt.rc('font', family='serif')
# Prepare Plot
plt.figure(figsize=(10,6), dpi=300)
plt.title(r"Linear Regression", fontsize=16)
plt.xlabel(r'$x$', fontsize=14)
plt.ylabel(r'$y$', fontsize=14)
# Plot with Legends
plt.scatter(x, y, label=r'$y=2x+1+\epsilon$', alpha=0.7)
plt.plot(x_reg, y_reg, label=r'$y={:.2f}x+{:.2f}$'.format(a, b))
# Other options
plt.legend(fontsize=12)
plt.grid()
plt.savefig("linear_reg.png", dpi=300)
이렇게 나온 그림은 다음과 같습니다.
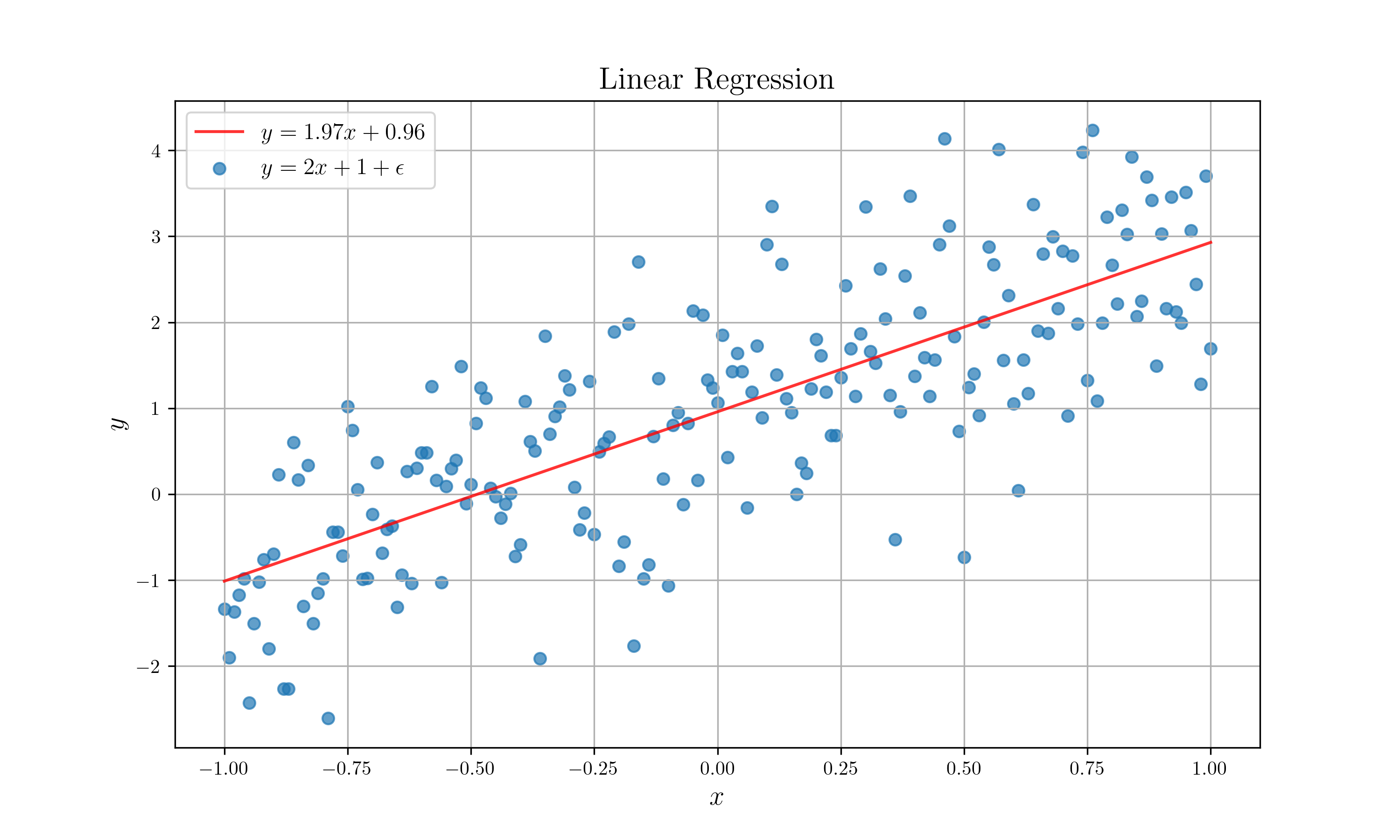
드디어 선형 회귀!
4. 마치며
최대한 간결하게 적으려 했는데, 내용이 내용이다보니 말이 많이 길어졌네요. 고등학교 과정에 국한해서 적다보니 빠진 내용들도 꽤 많은데, 혹시나 좀 더 공부하고 싶은 분들은 Bishop의 PRML을 보시는 것을 추천드립니다.
부록
1. 수학 성적 히스토그램 코드
// 1. Rust로 Data 생성하기
// https://git.io/JqXQb
extern crate peroxide;
use peroxide::fuga::*;
fn main() {
let n = Normal(60, 20); // 정규분포 생성
let y = n.sample(40) // 40개의 샘플 생성
.iter()
.map(|t| t.round()) // 반올림 (점수는 정수)
.filter(|x| *x <= 100f64) // 100점 이하만 채택
.collect();
let mut df = DataFrame::new(vec![]); // 데이터프레임 생성
df.push("y", Series::new(y)); // y 입력
df.print();
df.write_nc("data.nc") // netcdf 파일포맷으로 저장
.expect("Can't write nc");
}
# 2. Python으로 히스토그램 그리기
# https://git.io/JqX7Z
from netCDF4 import Dataset
import matplotlib.pyplot as plt
import seaborn as sns
# Import netCDF file
ncfile = './data.nc'
data = Dataset(ncfile)
var = data.variables
# Use latex
plt.rc('text', usetex=True)
plt.rc('font', family='serif')
# Prepare Histogram
plt.figure(figsize=(10,6), dpi=300)
plt.title(r"Math Score", fontsize=16)
plt.xlabel(r'Score', fontsize=14)
plt.ylabel(r'Density', fontsize=14)
# Prepare Data to Plot
y = var['y'][:]
# Draw Histogram
sns.distplot(y, label=r"Score", bins=10)
# Other options
plt.legend(fontsize=12)
plt.grid()
# Save
plt.savefig("hist.png", dpi=300)
2. 2020 수능 국어 등급컷 계산 코드
// Rust
// https://git.io/JqXHi
extern crate peroxide;
use peroxide::fuga::*;
fn main() {
let n = Normal(59.87, 20.22); // 정규분포 생성
(1f64 - n.cdf(91)).print(); // p(X >= 91) 계산
(1f64 - n.cdf(95)).print(); // p(X >= 95) 계산
}
3. 선형 모델 데이터 코드
# Julia
using NCDataFrame, DataFrames;
function f(x::S) where {T <: Number, S <: AbstractVector{T}}
2x .+ 1
end
x = -1.0:0.01:1.0;
ϵ = randn(length(x));
y = f(x) + ϵ;
df = DataFrame(x=x, y=y);
writenc(df, "linear.nc")
출처
[1] : 서울신문 - 올해의 과학 성과 1위는 ‘중력파’ 탐지
[2] : 메가스터디 - 역대 등급컷 공개
- C. Bishop, Pattern Recognition and Machine Learning (Information Science and Statistics), Springer-Verlag, 2006