6 분
🖊️ Rust와 미분하기 02: 기호 미분
🔖 Automatic Differentiation Series
📉 수치적 미분의 한계
저번 포스트에서 수치적 미분을 여러가지 방법으로 구현하는 것을 다뤄보았는데, 어떠셨나요? 아마, 코딩에 대한 조금의 지식만 있으면 오히려 고등학교때의 미분보다 훨씬 쉽게 느껴지셨을 겁니다. 저희가 사용한 것이라고는 그저 도함수의 정의에 따라 함수에 각 구간 값을 대입한 것이 전부였는데, 이를 코드로 나타내면 결국 다음의 코드에 지나지 않습니다.
# Python
def differentiation(f, x, h=1e-06):
return (f(x + h) - f(x)) / h
나머지는 이를 객체지향적으로 구현하거나, 함수형 프로그래밍으로 구현하거나 제너릭 프로그래밍을 도입하는 등의 구현방법의 차이일 뿐이었습니다. 이렇게 수치적 미분 방법은 굉장히 간단한 구현과 엄청 빠른 계산속도를 가져서 누구나 쉽게 미분을 할 수 있게 해주었습니다만, 오차가 필연적으로 발생하게 되는 단점이 있었습니다. 따라서 오차에 크게 민감하지 않은 문제나, Step 수가 적어서 오차가 크게 쌓이지 않는 미분방정식을 푸는 경우엔 충분하지만, 오차에 민감하거나 Step 수가 많아서 오차가 쌓여 유의미한 차이를 보여주는 미분방정식의 경우엔 큰 문제를 야기할 수 있습니다. 대표적인 예시로 “로렌즈의 나비"가 있습니다.
🦋 로렌즈의 나비
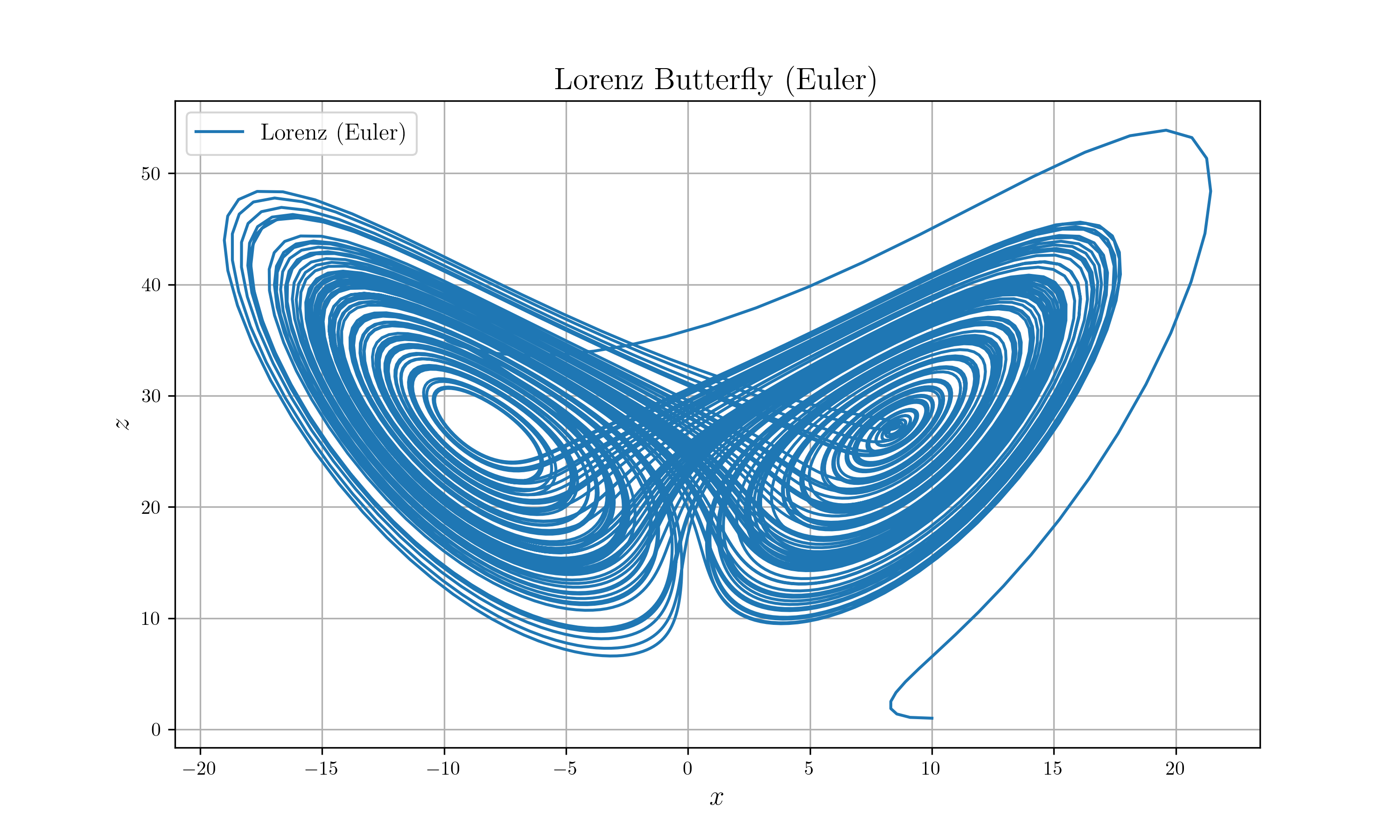
에드워드 로렌즈는 걸출한 수학자로, 특히 카오스 이론의 선구자로 유명하신 분입니다. 그는 1963년에 대기 대류의 간단한 수학적 모형을 만들었는데, 이 모델은 다음의 3개의 상미분방정식으로 이루어져 있습니다.
$$ \begin{align} \frac{dx}{dt} &= \sigma(y-x) \\ \frac{dy}{dt} &= x (\rho - z) - y \\ \frac{dz}{dt} &= xy - \beta z \end{align} $$
분명 아주 간단한 미분방정식인데, 놀랍게도 아주 복잡한 형태의 해가 도출됩니다. 이때의 대표적인 해의 형태가 위에서 첨부한 그림입니다. 이 시스템은 굉장히 예민한데, 매개변수의 값을 조금 바꾸거나 혹은 Step size를 조금만 바꿔도 해의 형태는 예측할 수 없는 형태로, 그것도 굉장히 파격적으로 변형됩니다. 예를 들어 위의 그림은 오일러(Euler) 방법이라는 수치적 미분방정식 해법 중 하나로 풀었는데, 위와 모든 조건을 동일하게 놓고 방법만 룽게-쿠타(Runge-Kutta 4th order) 방법으로 바꾸면 다음의 그림이 나옵니다.
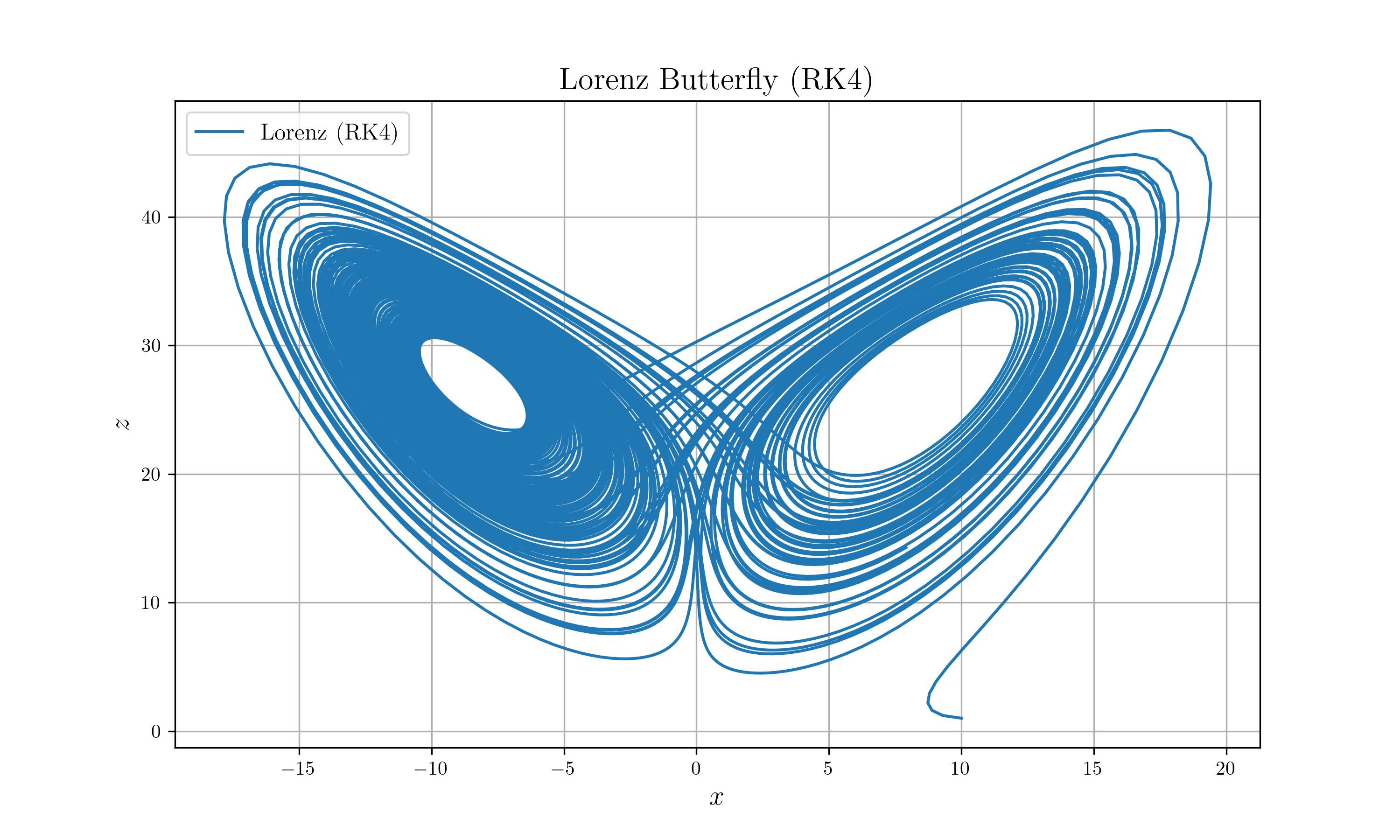
오로지 방법만 바꾸었을 뿐인데 결과가 상당히 많이 다른 것을 볼 수 있습니다. 물론 이 경우에는 전체적인 형태는 바뀌지 않지만, 특정 매개변수 주변에서는 아예 형태 전체가 급격하게 변형되는 경우도 발생합니다. 이러한 경우에는 오차가 필연적으로 발생하는 수치적 미분 방법이 적합하지 않습니다. 그렇다면 이런 경우에는 어떻게 풀어야 할까요?
🇬🇷 기호적 미분 (Symbolic Differentiation)
인간은 적절한 교육만 받는다면 미분을 아무런 오차없이 계산해낼 수 있습니다. (물론, 계산실수로 인한 오차는 종종 발생합니다.) 예를 들어 다음 함수의 도함수를 생각해봅시다.
$$ y = x^2 $$
이전 글에서 다루었다시피 수치적 미분 구현은 다음과 같습니다. 너무 똑같으면 심심하니 요즘 각광받는 수치 프로그래밍 언어인 Julia로 표현해보겠습니다.
# Julia
function df(x, f, h=1e-06)
return (f(x+h) - f(x)) / h
end
# Derivative
dx2(x) = df(x, x -> x^2)
# Print
println(dx2(1)) # 2.0000009999243673
이번엔 고등학생이 푸는 방법을 살펴봅시다. (대한민국 고등학교 2학년 수학2 과정을 이수한 학생이라고 가정합니다.)
$$ \begin{align} \frac{d}{dx}(x^2) &= \lim_{h \rightarrow 0} \frac{(x+h)^2 - x^2}{h} \\ &= \lim_{h\rightarrow 0} \frac{2hx + h^2}{h} \\ &= 2x \end{align} $$
여기에 1을 대입하면 정확히 2가 나옵니다. 위에서 수치적 미분의 결과와 달리 오차는 포함되지 않았습니다. 미분을 배운 사람일 경우, 위 풀이는 전혀 어려운 풀이가 아닙니다. 규칙만 잘 지킨다면 다른 함수들을 미분할 때에도 큰 어려움은 없을 겁니다.
물론 규칙이 조금 많긴 합니다 ㅎㅎ..
그렇다면 컴퓨터에게 규칙을 가르치면 어떨까요? 어떻게 가르치냐가 관건이겠지만 일단 가르칠 수 있다면 오차없는 완벽한 미분을 컴퓨터로 구현할 수 있을 것입니다. 다행히도 사람들은 이미 그것을 구현하였고 이를 CAS(Computer Algebra System)라 부릅니다.
대표적인 CAS로는 Mathematica, Matlab, Maple 등의 상업용 프로그램들과 Python으로 구현된 Sympy, Sagemath 등의 무료 프로그램 혹은 라이브러리가 있습니다. CAS는 실제로 인간이 하는 것처럼 미분, 적분, 대수 뿐 아니라 심지어 미분기하 등의 고급 수학 문제까지도 풀어낼 수 있습니다.
무려 이름도 SageManifolds 입니다.
아래는 sagemath를 이용한 간단한 도함수 구현입니다.
var('x') # 변수를 선언합니다.
f(x) = x^2 # 함수를 선언합니다.
df = diff(f, x) # 도함수를 계산합니다.
print(df(1)) # 2
정확할 뿐만 아니라 간단하기까지 하니 더 이상 수치적 미분을 고집할 이유는 없어보입니다. 하지만 이렇게 엄청난 CAS에도 치명적인 단점이 존재합니다. 바로 속도입니다. 기호적 미분 자체는 계산 속도가 빠를 수 있지만 그것에 수치 값들을 대입할 때 현저하게 속도 저하가 일어납니다. 아래는 간단한 미분 계산에 크기가 큰 배열 값을 대입하여 성능을 측정한 결과입니다. Peroxide는 Rust의 수치계산 라이브러리 이름이며 후에 다룰 자동미분 알고리즘을 적용하여 계산을 수행하였고, numpy는 Python의 유명한 수치계산 라이브러리로 수치적 미분으로 계산하였습니다. 마지막으로 Sagemath는 기호적 미분으로 계산 후 수치 값을 대입하여 결과를 구했습니다.
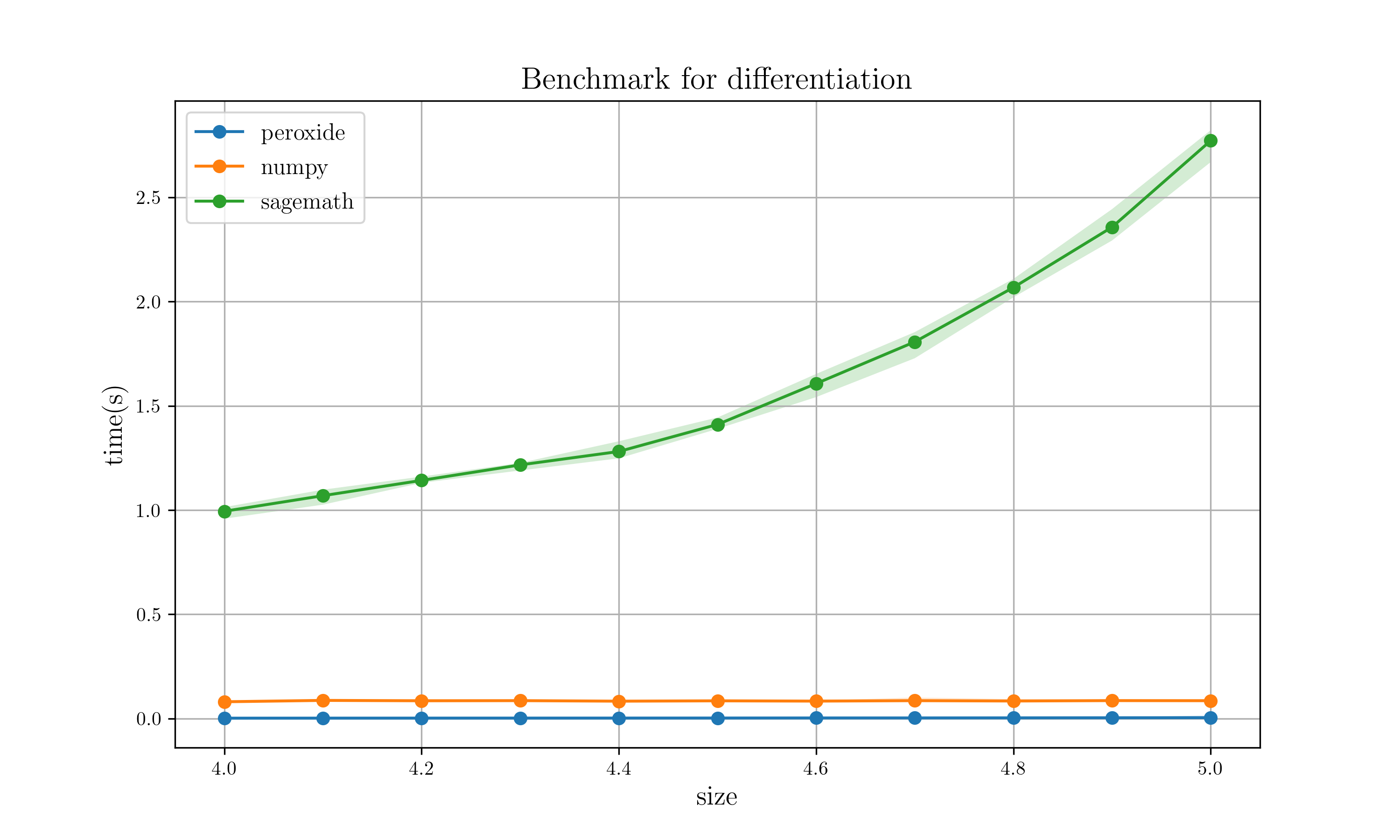
Linear scale 그래프입니다.
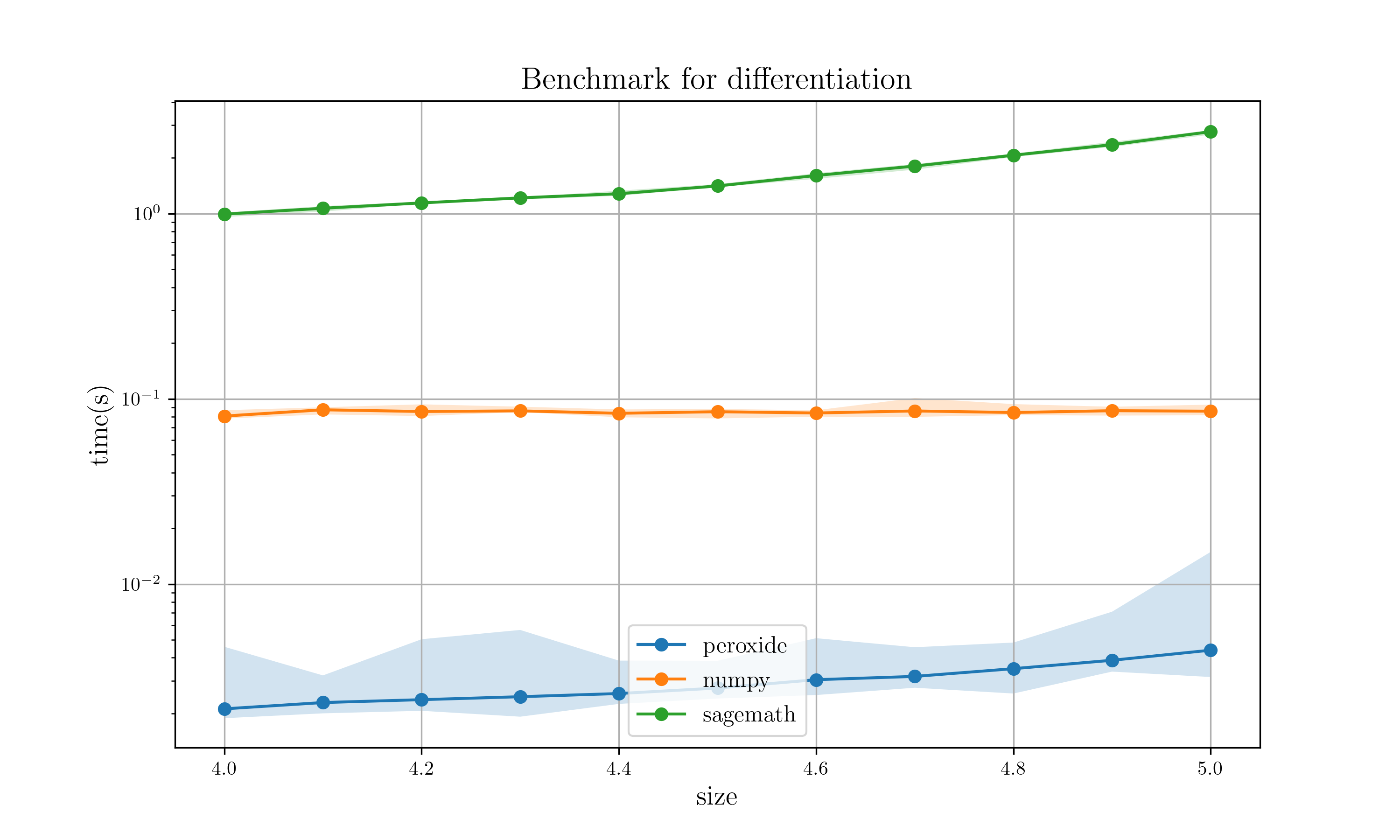
Log scale 그래프입니다.
물론 어떤 알고리즘을 사용했는지에 따라 실제 수치 계산에서의 결과는 조금 다를 수 있습니다. 다음은 Julia 언어 팀에서 실시한 Benchmark 결과입니다.

Log scale임을 참고하여 보시기 바랍니다. (출처: https://julialang.org/benchmarks/)
그림을 보면 Matlab의 오픈소스 격인 Octave는 예외로 치더라도 Mathematica가 생각보단 느리지 않음을 알 수 있습니다. (그래도 C보다 거의 10~100배 느리긴 하지만요.) Mathematica도 행렬 계산은 BLAS를 이용하고 갖가지 탁월한 수치 계산 알고리즘을 사용하기에 특정 계산들은 심지어 numpy를 이용한 Python보다 빠르기까지 합니다. 다만, Mathematica에서도 기호적 미분과 수치적인 연산을 서로 오갈때에는 역시나 큰 속도저하가 필연적으로 발생합니다.
그렇다면 규모가 큰 미분 계산에 대해서는 어떻게 접근해야할까요? 속도 저하를 고려하여 수치적 미분으로 구현하자니 규모가 커서 오차도 그만큼 많이 쌓일테고, 정확도를 고려하여 기호적 미분을 고려하자니 굉장히 오랜 시일이 걸릴 것은 뻔합니다. 심지어 메모리 문제로 게산 도중에 다운될 수도 있습니다. 다행히도 미분에 한해서는 거의 완벽한 해답이 존재합니다. 이에 대해서는 다음 포스트에서 다루도록 하겠습니다.
🔖 부록
A. 로렌즈 나비 코드
위에서 첨부한 로렌즈 나비 그림들은 Rust의 수치 라이브러리인 Peroxide를 이용하여 계산하였습니다. 소스코드는 다음과 같습니다.
extern crate peroxide;
use peroxide::fuga::*;
fn main() -> Result<(), Box<dyn Error>> {
// =========================================
// Declare ODE
// =========================================
let mut ex_test = ExplicitODE::new(butterfly);
let init_state: State<f64> = State::new(
0.0,
vec![10.0, 1.0, 1.0],
vec![0.0, 0.0, 0.0],
);
ex_test
.set_initial_condition(init_state)
.set_method(ExMethod::Euler)
.set_step_size(0.01f64)
.set_times(10000);
let mut ex_test2 = ex_test.clone();
ex_test2.set_method(ExMethod::RK4);
// =========================================
// Save results
// =========================================
let results = ex_test.integrate();
let results2 = ex_test2.integrate();
let mut df_euler = DataFrame::from_matrix(results);
df_euler.set_header(vec!["t", "x", "y", "z"]);
df_euler.print();
let mut df_rk4 = DataFrame::from_matrix(results2);
df_rk4.set_header(vec!["t", "x", "y", "z"]);
df_rk4.print();
df_euler.write_nc("data/euler.nc")?;
df_rk4.write_nc("data/rk4.nc")?;
Ok(())
}
fn butterfly(st: &mut State<f64>, _: &NoEnv) {
let x = &st.value;
let dx = &mut st.deriv;
dx[0] = 10f64 * (x[1] - x[0]);
dx[1] = 28f64 * x[0] - x[1] - x[0] * x[2];
dx[2] = -8f64/3f64 * x[2] + x[0] * x[1];
}
이후에 저장된 데이터를 불러와서 그림을 그리는 것은 Python으로 작성하였습니다. 코드는 다음과 같습니다.
from netCDF4 import Dataset
import matplotlib.pyplot as plt
# Import netCDF file
ncfile1 = './data/euler.nc'
data1 = Dataset(ncfile1)
var1 = data1.variables
ncfile2 = './data/rk4.nc'
data2 = Dataset(ncfile2)
var2 = data2.variables
# Use latex
plt.rc('text', usetex=True)
plt.rc('font', family='serif')
# Prepare Plot
plt.figure(figsize=(10,6), dpi=300)
plt.title(r"Lorenz Butterfly (Euler)", fontsize=16)
plt.xlabel(r'$x$', fontsize=14)
plt.ylabel(r'$z$', fontsize=14)
# Prepare Data to Plot
x1 = var1['x'][:]
z1 = var1['z'][:]
# Plot with Legends
plt.plot(x1, z1, label=r'Lorenz (Euler)')
# Other options
plt.legend(fontsize=12)
plt.grid()
plt.savefig("euler.png", dpi=300)
# Prepare Plot
plt.figure(figsize=(10,6), dpi=300)
plt.title(r"Lorenz Butterfly (RK4)", fontsize=16)
plt.xlabel(r'$x$', fontsize=14)
plt.ylabel(r'$z$', fontsize=14)
# Prepare Data to Plot
x2 = var2['x'][:]
z2 = var2['z'][:]
# Plot with Legends
plt.plot(x2, z2, label=r'Lorenz (RK4)')
# Other options
plt.legend(fontsize=12)
plt.grid()
plt.savefig("rk4.png", dpi=300)
이외에 자세한 사항은 Peroxide Gallery에 나와있으니 참고하시면 됩니다.