Bird's-EYE View of

Neutron Star Cooling

Tae Geun Kim

Yonsei HEP-COSMO

@ 16th Saga-Yonsei Joint Workshop

2019.12.23

Table OF CONTENTS

  • Introduce Neutron Star
  • Stellar Structure Equation
  • Equip with General Relativity
  • ERA of Computation
  • Mild blueprint

Stellar
structure Equation
 

stellar structure

What is a star?

  • Generate energy itself (Nuclear fusion)
  • Bound by self-gravity
  • Stable (via Hydrostatic equilibrium)

Stellar structure

How to describe a star?

Stellar structure equation

  1. Mass Conservation
  2. Hydrostatic equilibrium
  3. Energy transport
  4. Energy generation

+ Equation of State

Stellar structure

Conservation of Mass

\begin{aligned} &dm = 4\pi r^2 \rho dr \\ \Rightarrow ~&\dfrac{dm}{dr} = 4\pi r^2 \rho \end{aligned}
\delta dm = 0

Stellar structure

Hydrostatic Equilibrium

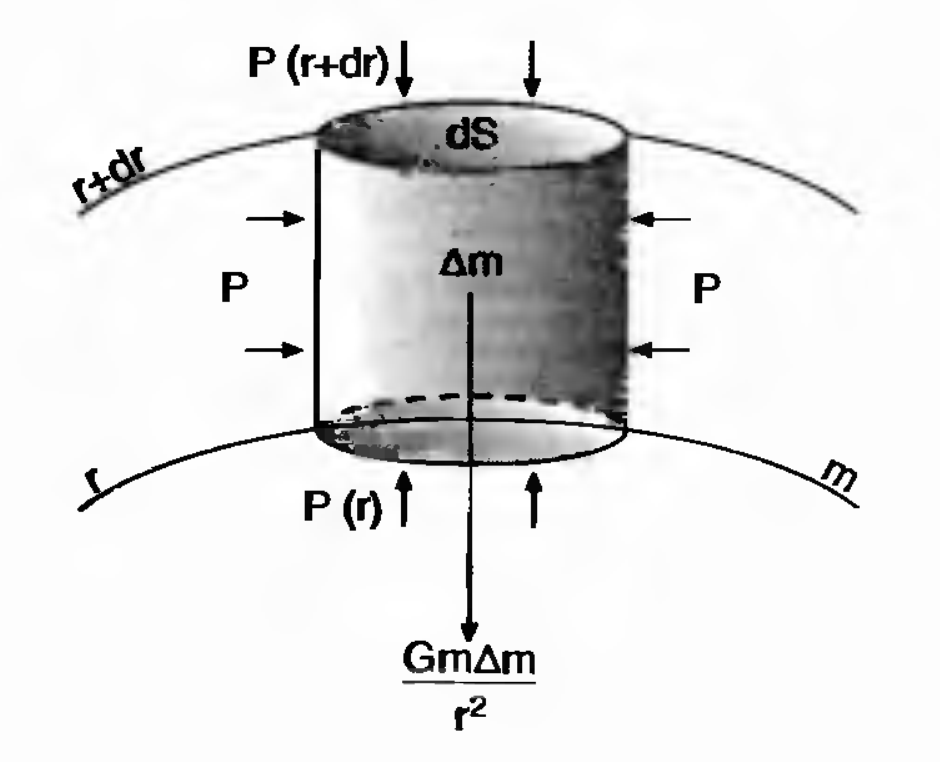
\begin{aligned} &F_g = - \dfrac{Gm\Delta m}{r^2},~~ \Delta m = \rho(r) dr dS \\ &F_P = P(r)dS - P(r+dr)dS = - \dfrac{dP}{dr}dr dS \\ \Rightarrow~& \Delta m \ddot{r} = F_g + F_P \\ \Rightarrow~&\ddot{r} = - \dfrac{Gm}{r^2} - \left(\dfrac{1}{\rho}\right)\dfrac{\partial P}{\partial r} \end{aligned}

If \( \ddot{r} \) = 0

\dfrac{dP}{dr} = - \rho \dfrac{Gm}{r^2}

Stellar structure

Total Energy

From 1st law of thermodynamics,

\delta(udm) = \delta u dm = \delta Q + \delta W
\begin{aligned} \delta W &= -P \delta dV = -P\delta \left(\dfrac{dV}{dm}dm\right) \\ &=-P \delta \left(\dfrac{1}{\rho}\right) dm \\ \\ \delta Q &= q dm \delta t + F(m) \delta t - F(m+dm)\delta t \\ &= \left(q - \dfrac{\partial F}{\partial m} \right)dm\delta t \end{aligned}

Equation becomes...

\dot{u} + P \dot{\left( \dfrac{1}{\rho} \right)} = q - \dfrac{\partial F}{\partial m}

Integrate with some tricks

\dot{U} + \dot{K} + \dot{\Omega} = L_{nuc} - L

For NS, \(\dot{K},\dot{\Omega},L_{nuc}=0\)

\dot{U} = C_v \dfrac{dT}{dt} = -L

Equip with

general relativity
 

setup geometry

For static, non-rotating and spherical symmetric star, we can write metric as follows

ds^2 = -e^{2\Phi(r)}dt^2 + e^{2\Lambda(r)}dr^2 + r^2 d\Omega^2

Consider perfect fluid matter.
From energy-momentum conservation (\(\nabla_\nu T^{\mu\nu} = 0 \)), we can obtain next equation.

\dfrac{dP}{dr} = - (\rho + P) \dfrac{d\Phi}{dr}

From Einstein equation, we can get below relations.

e^{-2\Lambda(r)} = 1 - \dfrac{2m(r)}{r}
\dfrac{d\Phi}{dr} = -\dfrac{1}{\rho}\dfrac{dP}{dr}\left(1 + \dfrac{P}{\rho}\right)^{-1}

Tolman-oppenheimer-volkoff equation

\begin{aligned} \dfrac{dm}{dr} &= 4\pi r^2 \rho \\ \dfrac{dP}{dr} &= - \dfrac{\rho m}{r^2} \left( 1 + \dfrac{P}{\rho}\right) \left(1 + \dfrac{4\pi P r^3}{m}\right) \left(1 - \frac{2m}{r} \right)^{-1} \end{aligned}

Combine all equations of previous slides, then we can get next equations.

These equation is called TOV equation. (already appeared in Prof. Tachibana's lecture)

Newtonian VS General Relativity

\begin{aligned} \dfrac{dm}{dr} &= 4\pi r^2 \rho \\ \dfrac{dP}{dr} &= - \dfrac{\rho m}{r^2} \left( 1 + \dfrac{P}{\rho}\right) \left(1 + \dfrac{4\pi P r^3}{m}\right) \left(1 - \frac{2m}{r} \right)^{-1} \end{aligned}
\begin{aligned} \dfrac{dm}{dr} &= 4\pi r^2 \rho \\ \dfrac{dP}{dr} &= - \dfrac{\rho m}{r^2} \end{aligned}

Newtonian

General Relativity

C_v \dfrac{dT}{dt} = - (L+L_{etc})
\begin{aligned} \dfrac{dT}{dr} &= - \dfrac{3}{4ac} \dfrac{\kappa \rho}{T^3} \dfrac{L}{4\pi r^2} \\ \dfrac{dL}{dr} &= 4\pi r^2 \rho q \end{aligned}
\begin{aligned} \dfrac{d(Te^\Phi)}{dr} &= - \dfrac{1}{\lambda} \dfrac{Le^\Phi}{4\pi r^2 \sqrt{1 - 2m/r}} \\ \dfrac{d(Le^{2\Phi})}{dr} &= - \dfrac{4\pi r^2 e^\Phi}{\sqrt{1 - 2m/r}}\left( C_v \dfrac{dT}{dt} + e^\Phi(Q_\nu + Q_{etc})\right) \end{aligned}

ERA of computation
 

overview of computation process for
neutron star cooling

  1. Set initial condition - \(\rho_c\)
  2. Choose Equation of State - \(P=P(\rho)\)
  3. Solve TOV equation - \(m(r),\Phi(r),\rho(r),P(r)\)
  4. Determine & calculate neutrino & photon emissivity - \(Q_\nu, Q_\gamma\)
  5. Numerically solve system of differential equations - \(L,T\)

It seems to be easy to implement.

Too many things to do

two candidates

NSCool (D. Page)
dStar (E. F. Brown)
  • Pros
    • Stand-alone (No external dependencies)
    • Have experiences working with Particle Physics (By Koichi Hamaguchi)

  • Cons

    • Too old (Fortran 77)

    • Contains some errors

    • Contains deprecated codes

    • No any documentation

  • Pros
    • Reliable (Built on MESA)
    • Readable & Relatively easy to use
      (Modern Fortran)
    • Opensource (on Github)
  • Cons
    • Should study MESA first
    • Nobody used this code for particle physics related research

My Process

Now, I'm working with NSCool. But hard to customize & still some errors.
\(\Rightarrow \) Porting to effective modern platform with some modification - Rust

- Much side-effects, not pure subroutine

Raw coding

- Not much side-effects, pure subroutine

extern
ffi

mild
blueprint
 

Brief_plan.py
research = ResearchStatus.get()

while True:
  while research != "porting complete":
    research.more()
    time.sleep(0)

  # Is it valid with observation data?
  if research.valid_with_data():
    research.go_to_next_phase()
    break
  else:
    research = ResearchStatus.error()
    continue

Current status

Describe Neutron star

via TOV

Understand Fermi gas theory

Complete porting of NSCool

Test with observed data

Start particle physics related research

Current status

expectation

  • Can understand cooling process of Neutron star.
  • Have effective research framework which contains following properties.
    • Reduce error between theory & simulation.
    • Do not have to suffer with architecture dependencies.
    • More safe & more fast.
    • Complete documentation.
    • Easy to use.

references

  • Astrophysics Books
    • Stellar evolution
      • Prialnik, D. (2000). An introduction to the theory of stellar structure and evolution. Cambridge: Cambridge University Press.
    • Compact Star
      • Glendenning, N. K. (1997). Compact stars: Nuclear physics, particle physics, and general relativity. New York: Springer.
  • Articles
    • Neutron Star Cooling

      • Potekhin, Alexander Y., José A. Pons, and Dany Page. Neutron Stars—Cooling and Transport. Space Science Reviews 191.1-4 (2015): 239–291. Crossref. Web.

Thank you

for

Listening