Module spline

Source

Expand description

Spline interpolations

§Available splines

Cubic spline
Cubic Hermite spline
B-spline

§`Spline<T>` trait

§Methods

fn eval(&self, t: f64) -> T : Evaluate the spline at t
- For Cubic Spline, t means x (domain) and T = f64
- For B-Spline, t means parameter of curve and T = (f64, f64)
fn eval_vec(&self, v: &[f64]) -> Vec<T> : Evaluate spline values for an array v
fn eval_with_cond<F>(&self, t: f64, cond: F) -> T : Evaluate the spline at t, with a condition
fn eval_vec_with_cond<F>(&self, v: &[f64], cond: F) -> Vec<T> : Evaluate spline values for an array v, with a condition

§`PolynomialSpline` trait

§Methods

fn polynomial_at(&self, x: f64) -> &Polynomial : Get the polynomial at x
fn number_of_polynomials(&self) -> usize : Get the number of polynomials
fn get_ranged_polynomials(&self) -> &Vec<(Range<f64>, Polynomial)> : Get the polynomials

§Low-level interface

§Members

CubicSpline: Structure for cubic spline
- fn from_nodes(node_x: &[f64], node_y: &[f64]) -> Result<Self> : Create a cubic spline from nodes
- fn extend_with_nodes(&mut self, node_x: Vec<f64>, node_y: Vec<f64>) -> Result<()> : Extend the spline with nodes
CubicHermiteSpline: Structure for cubic Hermite spline
- fn from_nodes_with_slopes(node_x: &[f64], node_y: &[f64], m: &[f64]) -> Result<Self> : Create a Cubic Hermite spline from nodes with slopes
- fn from_nodes(node_x: &[f64], node_y: &[f64], slope_method: SlopeMethod) -> Result<Self> : Create a Cubic Hermite spline from nodes with slope estimation methods
- SlopeMethod: Enum for slope estimation methods
  - Akima: Akima’s method to estimate slopes (Akima (1970))
  - Quadratic: Using quadratic interpolation to estimate slopes
BSpline: Structure for B-Spline
- fn open(degree: usize, knots: Vec<f64>, control_points: Vec<Vec<f64>>) -> Result<Self> : Create an open B-Spline
- fn clamped(degree: usize, knots: Vec<f64>, control_points: Vec<Vec<f64>>) -> Result<Self> : Create a clamped B-Spline
- fn cox_de_boor(t: f64, i: f64) : Cox-de Boor recursion formula (Here, use iteration instead of recursion)

§Usage (Cubic Spline Family)

use peroxide::fuga::*;

fn main() -> Result<(), Box<dyn Error>> {
    let x = seq(0, 10, 1);
    let y = x.fmap(|t| t.sin());
     
    let cs = CubicSpline::from_nodes(&x, &y)?;
    let cs_akima = CubicHermiteSpline::from_nodes(&x, &y, Akima)?;
    let cs_quad = CubicHermiteSpline::from_nodes(&x, &y, Quadratic)?;

    cs.polynomial_at(0f64).print();
    cs_akima.polynomial_at(0f64).print();
    cs_quad.polynomial_at(0f64).print();
    // -0.1523x^3 + 0.9937x
    // 0.1259x^3 - 0.5127x^2 + 1.2283x
    // -0.0000x^3 - 0.3868x^2 + 1.2283x

    let new_x = seq(4, 6, 0.1);
    let new_y = new_x.fmap(|t| t.sin());

    let y_cs = cs.eval_vec(&new_x);
    let y_akima = cs_akima.eval_vec(&new_x);
    let y_quad = cs_quad.eval_vec(&new_x);

    let mut df = DataFrame::new(vec![]);
    df.push("x", Series::new(new_x));
    df.push("y", Series::new(new_y));
    df.push("y_cs", Series::new(y_cs));
    df.push("y_akima", Series::new(y_akima));
    df.push("y_quad", Series::new(y_quad));

    df.print();
    //          x       y    y_cs y_akima  y_quad
    //  r[0]    5 -0.9589 -0.9589 -0.9589 -0.9589
    //  r[1]  5.2 -0.8835 -0.8826 -0.8583 -0.8836
    //  r[2]  5.4 -0.7728 -0.7706 -0.7360 -0.7629
    //  r[3]  5.6 -0.6313 -0.6288 -0.5960 -0.6120
    //  r[4]  5.8 -0.4646 -0.4631 -0.4424 -0.4459
    //  r[5]    6 -0.2794 -0.2794 -0.2794 -0.2794

    Ok(())
}

§Usage (B-Spline)

use peroxide::fuga::*;

fn main() -> Result<(), Box<dyn Error>> {
    let knots = vec![0f64, 1f64, 2f64, 3f64];
    let degree = 3;
    let control_points = vec![
        vec![0f64, 2f64],
        vec![0.2, -1f64],
        vec![0.4, 1f64],
        vec![0.6, -1f64],
        vec![0.8, 1f64],
        vec![1f64, 2f64],
    ];

  
    let spline = BSpline::clamped(degree, knots, control_points.clone())?;
    let t = linspace(0f64, 3f64, 200);
    let (x, y): (Vec<f64>, Vec<f64>) = spline.eval_vec(&t).into_iter().unzip();

        let control_x = control_points.iter().map(|v| v[0]).collect::<Vec<f64>>();
        let control_y = control_points.iter().map(|v| v[1]).collect::<Vec<f64>>();

        let mut plt = Plot2D::new();
        plt
            .insert_pair((x.clone(), y.clone()))
            .insert_pair((control_x.clone(), control_y.clone()))
            .set_plot_type(vec![(1, PlotType::Scatter)])
            .set_color(vec![(0, "darkblue"), (1, "red")])
            .set_xlabel(r"$x$")
            .set_ylabel(r"$y$")
            .set_style(PlotStyle::Nature)
            .set_dpi(600)
            .set_path("example_data/b_spline_test.png")
            .savefig()?;

    let mut df = DataFrame::new(vec![]);
    df.push("t", Series::new(t));
    df.push("x", Series::new(x));
    df.push("y", Series::new(y));
    df.print();

    Ok(())
}

Result for above code is:

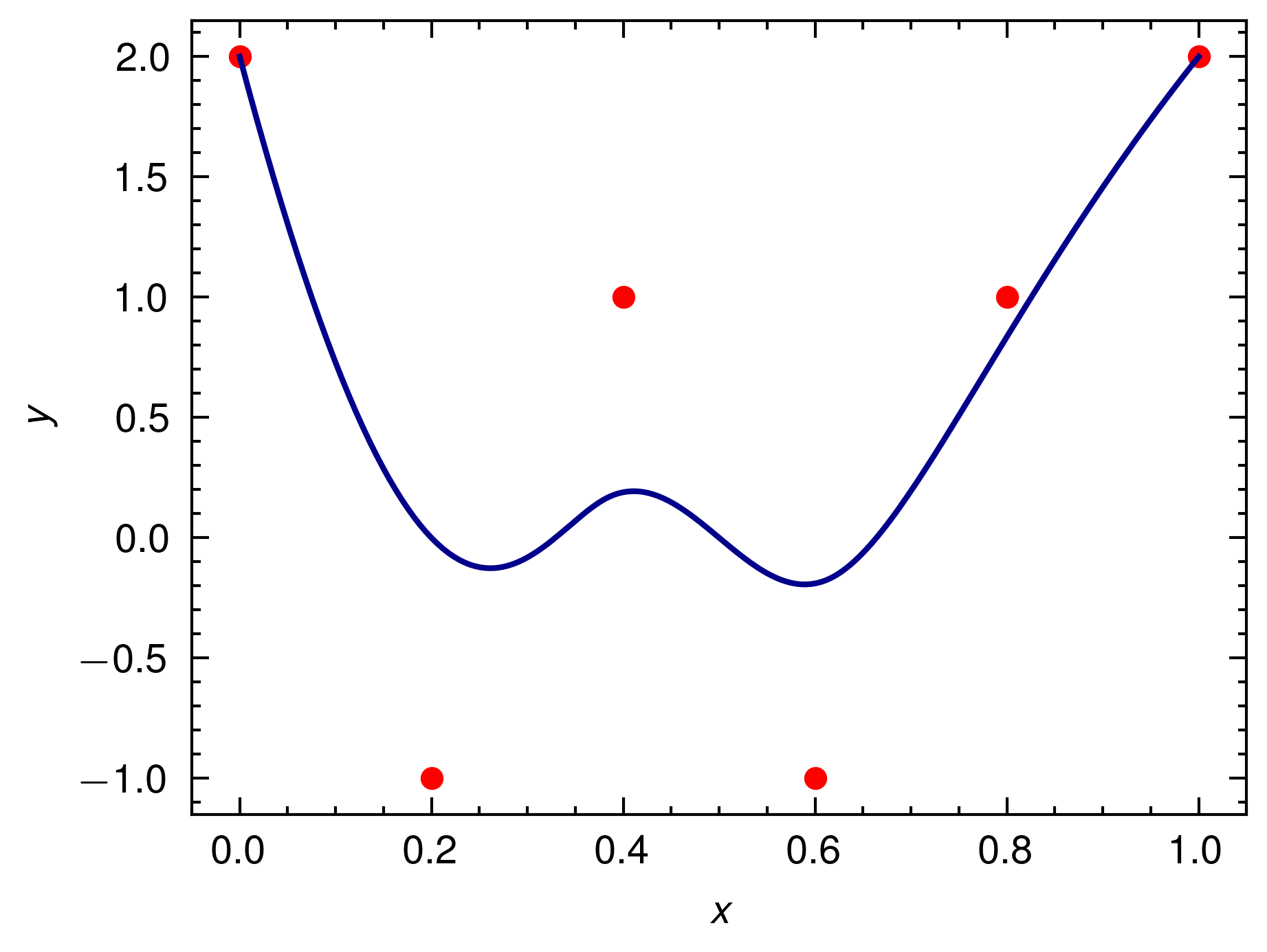
§High-level interface

§Functions

fn cubic_spline(node_x: &[f64], node_y: &[f64]) -> CubicSpline : Create a cubic spline from nodes
fn cubic_hermite_spline(node_x: &[f64], node_y: &[f64], m: &[f64]) -> CubicHermiteSpline : Create a cubic Hermite spline from nodes with slopes

§Usage

use peroxide::fuga::*;

fn main() -> Result<(), Box<dyn Error>> {
    let x = seq(0, 10, 1);
    let y = x.fmap(|t| t.sin());
     
    let cs = cubic_spline(&x, &y)?;
    let cs_akima = cubic_hermite_spline(&x, &y, Akima)?;
    let cs_quad = cubic_hermite_spline(&x, &y, Quadratic)?;

    cs.polynomial_at(0f64).print();
    cs_akima.polynomial_at(0f64).print();
    cs_quad.polynomial_at(0f64).print();
    // -0.1523x^3 + 0.9937x
    // 0.1259x^3 - 0.5127x^2 + 1.2283x
    // -0.0000x^3 - 0.3868x^2 + 1.2283x

    let new_x = seq(4, 6, 0.1);
    let new_y = new_x.fmap(|t| t.sin());

    let y_cs = cs.eval_vec(&new_x);
    let y_akima = cs_akima.eval_vec(&new_x);
    let y_quad = cs_quad.eval_vec(&new_x);

    let mut df = DataFrame::new(vec![]);
    df.push("x", Series::new(new_x));
    df.push("y", Series::new(new_y));
    df.push("y_cs", Series::new(y_cs));
    df.push("y_akima", Series::new(y_akima));
    df.push("y_quad", Series::new(y_quad));

    df.print();
    //          x       y    y_cs y_akima  y_quad
    //  r[0]    5 -0.9589 -0.9589 -0.9589 -0.9589
    //  r[1]  5.2 -0.8835 -0.8826 -0.8583 -0.8836
    //  r[2]  5.4 -0.7728 -0.7706 -0.7360 -0.7629
    //  r[3]  5.6 -0.6313 -0.6288 -0.5960 -0.6120
    //  r[4]  5.8 -0.4646 -0.4631 -0.4424 -0.4459
    //  r[5]    6 -0.2794 -0.2794 -0.2794 -0.2794

    Ok(())
}

§Calculus with polynomial splines

§Usage

use peroxide::fuga::*;
use std::f64::consts::PI;

fn main() -> Result<(), Box<dyn Error>> {
    let x = seq(0, 10, 1);
    let y = x.fmap(|t| t.sin());
     
    let cs = cubic_spline(&x, &y)?;
    let cs_akima = cubic_hermite_spline(&x, &y, Akima)?;
    let cs_quad = cubic_hermite_spline(&x, &y, Quadratic)?;

    println!("============ Polynomial at x=0 ============");

    cs.polynomial_at(0f64).print();
    cs_akima.polynomial_at(0f64).print();
    cs_quad.polynomial_at(0f64).print();

    println!("============ Derivative at x=0 ============");

    cs.derivative().polynomial_at(0f64).print();
    cs_akima.derivative().polynomial_at(0f64).print();
    cs_quad.derivative().polynomial_at(0f64).print();

    println!("============ Integral at x=0 ============");

    cs.integral().polynomial_at(0f64).print();
    cs_akima.integral().polynomial_at(0f64).print();
    cs_quad.integral().polynomial_at(0f64).print();

    println!("============ Integrate from x=0 to x=pi ============");

    cs.integrate((0f64, PI)).print();
    cs_akima.integrate((0f64, PI)).print();
    cs_quad.integrate((0f64, PI)).print();

    // ============ Polynomial at x=0 ============
    // -0.1523x^3 + 0.9937x
    // 0.1259x^3 - 0.5127x^2 + 1.2283x
    // -0.0000x^3 - 0.3868x^2 + 1.2283x
    // ============ Derivative at x=0 ============
    // -0.4568x^2 + 0.9937
    // 0.3776x^2 - 1.0254x + 1.2283
    // -0.0000x^2 - 0.7736x + 1.2283
    // ============ Integral at x=0 ============
    // -0.0381x^4 + 0.4969x^2
    // 0.0315x^4 - 0.1709x^3 + 0.6141x^2
    // -0.0000x^4 - 0.1289x^3 + 0.6141x^2
    // ============ Integrate from x=0 to x=pi ============
    // 1.9961861265456702
    // 2.0049920614062775
    // 2.004327391790717

    Ok(())
}

§B-Spline utils

UnitCubicBasis: Single cubic B-Spline basis function
CubicBSplineBases: Uniform Cubic B-Spline basis functions

§References

Gary D. Knott, Interpolating Splines, Birkhäuser Boston, MA, (2000).

Structs§

ArchivedBSpline: An archived BSpline
ArchivedCubicBSplineBases: An archived CubicBSplineBases
ArchivedCubicHermiteSpline: An archived CubicHermiteSpline
ArchivedCubicSpline: An archived CubicSpline
ArchivedUnitCubicBasis: An archived UnitCubicBasis
BSpline: B-Spline
BSplineResolver: The resolver for an archived BSpline
CubicBSplineBases: Uniform Cubic B-Spline basis functions
CubicBSplineBasesResolver: The resolver for an archived CubicBSplineBases
CubicHermiteSpline
CubicHermiteSplineResolver: The resolver for an archived CubicHermiteSpline
CubicSpline: Cubic Spline (Natural)
CubicSplineResolver: The resolver for an archived CubicSpline
UnitCubicBasis: Unit Cubic Basis Function
UnitCubicBasisResolver: The resolver for an archived UnitCubicBasis

Enums§

SlopeMethod
SplineError

Traits§

PolynomialSpline
Spline

Functions§

cubic_hermite_spline
cubic_spline: Cubic Spline (Natural)

Module splineCopy item path

§Available splines

§Spline<T> trait

§Methods

§PolynomialSpline trait

§Methods

§Low-level interface

§Members

§Usage (Cubic Spline Family)

§Usage (B-Spline)

§High-level interface

§Functions

§Usage

§Calculus with polynomial splines

§Usage

§B-Spline utils

§References

Structs§

Enums§

Traits§

Functions§

Module spline

§`Spline<T>` trait

§`PolynomialSpline` trait